「結合」「整理」「分離」の3つのルールで群れの動きを表現します。
結合(Cohesion)

周囲(視野範囲内)のユニットの平均位置に向かうベクトル。
このベクトルによって互いを引き合って集団を形成することができます。
整理(Alignment)

周囲のユニットの平均方向のベクトル。
集団がかたまりになって動く方向になります。
分離(Separation)
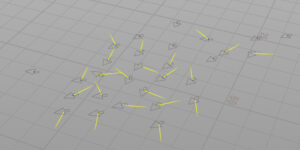
周囲のユニットに近づきすぎている場合に離れる方向のベクトル。
このベクトルのおかげでユニット同士が一定の距離を保つことができます。近いユニットに対して逆方向のベクトルを累積し、距離が近いものほど強めにします。
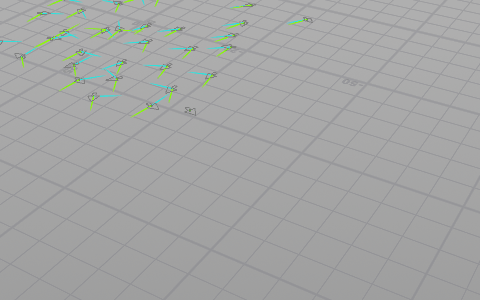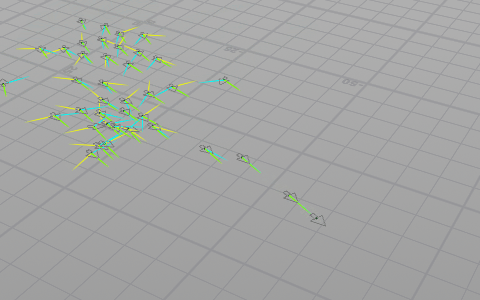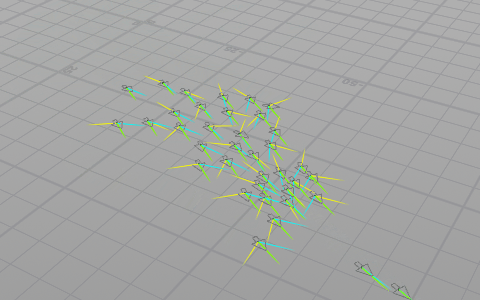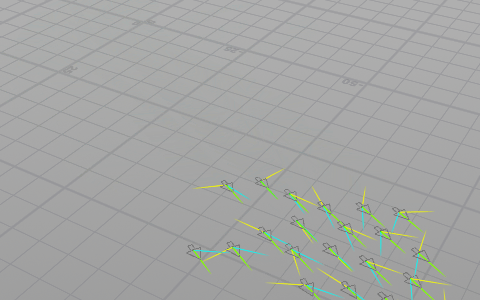
この3つのベクトルを合成した結果を進む方向とします。スムーズに動かすためにこの方向へユニットを回転(操舵)させながら進ませます。
範囲
周囲のユニットを探すための視野と半径を設定します。
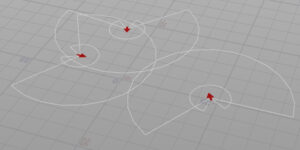
ひとつでもよかったのかもしれませんが「結合と整理」と「分離」で分けました。分離は近づきすぎた相手から離れるための範囲なので小さめに設定しています。
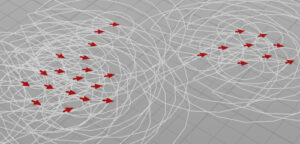
視野角を広くするとまとまって動き、
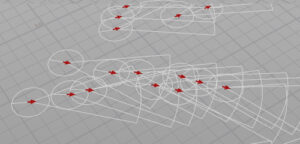
視野角を狭くすると行列のような動きになります。面白いですね。
必要なパラメータ
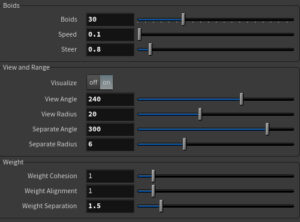
操作するUIはこのようにしてみました。
以下Houdiniで書いてみたコード。
まずは初期化(UIから値を拾っています)
// Run Over: Points
// 初期のベクトル
float angle = radians(rand(@ptnum)*360);
@N = normalize(set(cos(angle), 0, sin(angle)));
@up = set(0, 1, 0);
// 速度
f@speed = `chs("../controller/speed")`;
// 操舵力
f@steer = radians(`chs("../controller/steer")`);
// 距離
f@viewRadius = `chs("../controller/viewRadius")`;
// 視野角
f@viewAngle = `chs("../controller/viewAngle")`;
// 分離(距離)
f@separateRadius = `chs("../controller/separateRadius")`;
// 分離(視野角)
f@separateAngle = `chs("../controller/separateAngle")`;
// 重み
f@weightCohesion = `chs("../controller/weightCohesion")`;
f@weightAlignment = `chs("../controller/weightAlignment")`;
f@weightSeparation = `chs("../controller/weightSeparation")`;つぎにSolver SOP内のWrangleです。毎フレームこの計算で座標が更新されます。
// Run Over: Points
// 範囲内のユニット数
int num = 0;
// ベクトルを累積するための変数
vector avgP = set(0, 0, 0);
vector avgN = set(0, 0, 0);
vector avgS = set(0, 0, 0);
for(int i = 0; i < npoints(0); i++)
{
if(i != @ptnum)
{
// 対象ユニットの座標
vector targetP = point(0, "P", i);
// 結合と整列
// 視野範囲内か
if(dot(@N, normalize(targetP - @P)) > cos(radians(f@viewAngle/2)))
{
// 半径内か
vector toTarget = targetP - @P;
if((toTarget.x * toTarget.x + toTarget.z * toTarget.z) < f@viewRadius * f@viewRadius)
{
// 対象ユニットの方向ベクトル
vector targetN = point(0, "N", i);
// 結合
avgP += targetP;
// 整列
avgN += targetN;
num++;
}
}
// 分離
// 視野範囲内か
if(dot(@N, normalize(targetP - @P)) > cos(radians(f@separateAngle/2)))
{
// 半径内か
float dist = length(targetP - @P);
if(dist < f@separateRadius)
{
float mag = dist / f@separateRadius;
avgS += normalize(@P - targetP) * (1 - mag);
}
}
}
}
// 進行ベクトルを計算する
if(num > 0)
{
// ユニット数で割って平均のベクトルにする
avgP /= float(num);
avgN /= float(num);
vector vecCohesion = normalize(avgP - @P);
vector vecAlignment = normalize(avgN);
vector vecSeparation = normalize(avgS);
// 3つのベクトルを合成(重みづけもする)
vector vecResult = normalize(vecCohesion * f@weightCohesion + vecAlignment * f@weightAlignment + vecSeparation * f@weightSeparation);
// 向いている方角と結果のベクトルの角度差を計算
float angle = acos(dot(@N, vecResult));
// 操舵力以上の回転値にしないようにクランプする
angle = min(f@steer, angle);
// 外積からもうひとつの軸を計算する
v@left = cross(@up, @N);
// 内積の符号を取得
float d = dot(vecResult, v@left);
if(d < 0) angle *= -1;
// クォータニオンで回転
vector4 q = quaternion(angle, @up);
@N = qrotate(q, @N);
}
// 座標の更新
@P += @N * f@speed;こんなシンプルなコードでもしっかり群衆らしく動くので驚きました。拡張すればさらに複雑な動きも表現できそうですね。