重力加速度だけでカーブ上を走らせる計算です。

カーブの準備
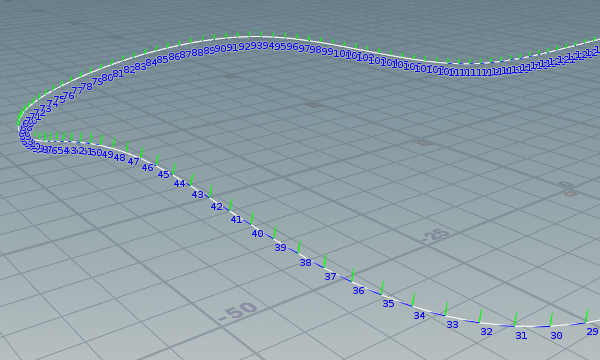
進行ベクトルを@Nに、車両を傾ける上方向のベクトルを@upに格納しておく。このカーブから傾きを取得して車両の姿勢に反映させる。
重力
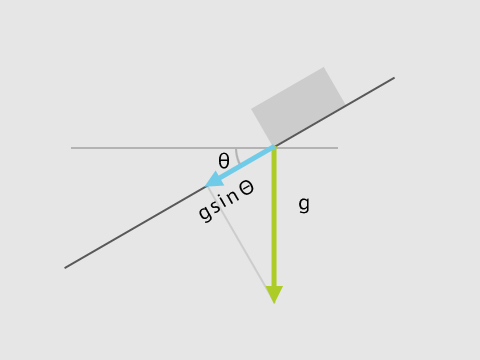
加速度はg*sinΘとなる。Θはカーブの進行ベクトルの高さと底辺の長さからアークタンジェントで計算する。
Solver SOP内のWrangleコード
座標計算はカーブの一次元の位置を進めるだけで、三次元の座標はprimuv()でカーブから取得する。
// Run Over: Point
// input1: curve
// 進行ベクトルから角度を求める(高さとXZ平面の長さからアークタンジェントで求める)
float theta = atan2(v@N.y, sqrt(v@N.x * v@N.x + v@N.z * v@N.z));
// 重力加速度(1秒を60フレームで描画するので時間の平方で割る)
float gravity = (9.8 / float(60 * 60)) * -1;
// 速度に加算
f@speed += gravity * sin(theta);
// 摩擦係数(摩擦で減速させたければ0.995等の数字を入れる)
float friction = 1;
f@speed *= friction;
// カーブにおける位置に速度を加算する
f@curvePos += f@speed;
// カーブの長さ
float curveLength = primintrinsic(1, "measuredperimeter", 0);
// パラメトリックUVの座標をつくる(0-1にスケールする)
float ratio = (f@curvePos / curveLength) % 1;
vector2 posuv = set(ratio, 0);
// UVからカーブ上の座標を取得する
@P = primuv(1, "P", 0, posuv);
// 同じようにカーブからNとupベクトルを取得する
@N = primuv(1, "N", 0, posuv);
@up = primuv(1, "up", 0, posuv);このポイントにCopy to Points SOPで車両メッシュを配置している。

重力だけで走っているので、開始地点より高い位置には行けずに重力に負けて逆走している。
フレームあたりの重力の値
60フレームで動かす場合、重力は1秒の9.8mではなく、9.8/(60*60)mになる。
例えば物を落として5秒後の距離は1/2*g*5^2となるが、5秒=5*60フレームと考えると、1/2*g*(5*60)^2となるので、gを60^2で割るとつじつまが合って同じ距離になる。