平面上の3点を通る円の中心座標と半径の求め方。
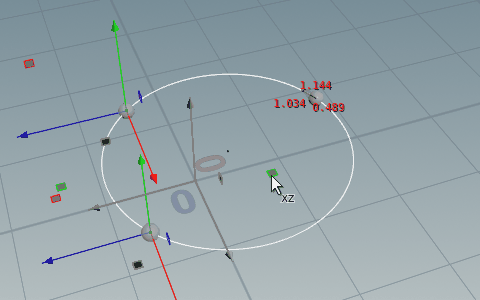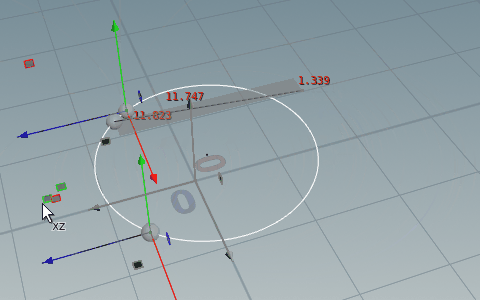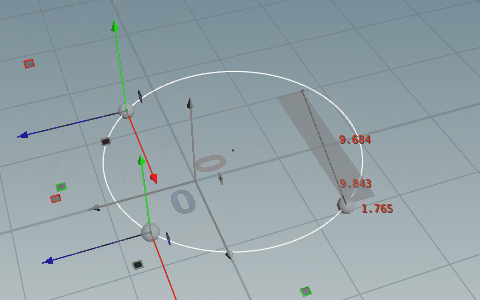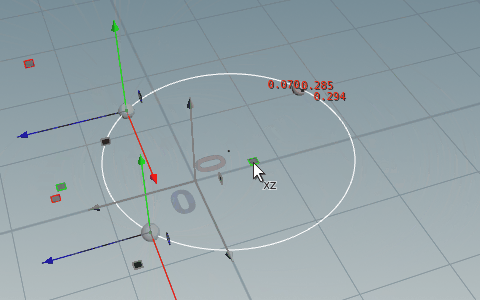
// Run Over: Detail
// 3点を通る円の中心点と半径を求める
//
// 行列式
float det(vector a; vector b; vector c;)
{
return a.x*b.y*c.z + a.z*b.x*c.y + a.y*b.z*c.x - a.z*b.y*c.x - a.y*b.x*c.z - a.x*b.z*c.y;
}
// input0に入力された3点を使う
vector p0 = point(0, "P", 0);
vector p1 = point(0, "P", 1);
vector p2 = point(0, "P", 2);
vector a = set(p0.x, p1.x, p2.x);
vector b = set(p0.z, p1.z, p2.z);
vector c = set(1, 1, 1);
vector d = set(-(p0.x * p0.x) - (p0.z * p0.z), -(p1.x * p1.x) - (p1.z * p1.z), -(p2.x * p2.x) - (p2.z * p2.z));
float l = det(d, b, c) / det(a, b, c);
float m = det(a, d, c) / det(a, b, c);
float n = det(a, b, d) / det(a, b, c);
// 中心点
addpoint(0, set(-l/2, 0, -m/2));
// 中心座標と半径
v@center = set(-l/2, 0, -m/2);
f@radius = sqrt((l*l + m*m - 4*n) / 4);コードの解説
原点を通る半径4の円の式は
x2 + y2 = 16
点(-5, 3)を通る半径4の円の式は
(x + 5)2 + (y – 3)2 = 16
となる。これを展開すると
x2 + y2 + 10x + 6y + 18 = 0
つまり求める円の方程式は x2 + y2 + lx + my + n = 0 という形になる。
l, m, nを求める
これを一次関数 ax + by + cz = d の形にすると
lx + my + n = -x2 – y2
3頂点の座標をx,yに入力して3つの一次関数の式をつくりクラメル式で解く。
3頂点をそれぞれp0, p1, p2とすると
p0.x * l + p0.z * m + 1 * n = -p0.x2 – p0.z2
p1.x * l + p1.z * m + 1 * n = -p1.x2 – p1.z2
p2.x * l + p2.z * m + 1 * n = -p2.x2 – p2.z2
となるので、
a = (p0.x, p1.x, p2.x)
b = (p0.z, p1.z, p2.z)
c = (1, 1, 1)
d = (-p0.x2 – p0.z2, -p1.x2 – p1.z2, -p2.x2 – p2.z2)
行列式でそれぞれを求める
l = det(d, b, c) / det(a, b, c)
m = det(a, d, c) / det(a, b, c)
n = det(a, b, d) / det(a, b, c)
中心座標と半径の式
x2 + y2 + lx + my + n = 0 を円の方程式 (x-a)2 + (y-b)2 = r2 の形にする。
x2 + y2 + lx + my + n = 0 を平方完成すると (x + l/2)2 + (y + m/2)2 = (l2 + m2 – 4n)/4 となるので、中心座標は (-l/2, -m/2) になり、半径はsqrt((l2 + m2 – 4n)/4) となる。
先ほどのl、m、nの値を代入すれば求まる。

