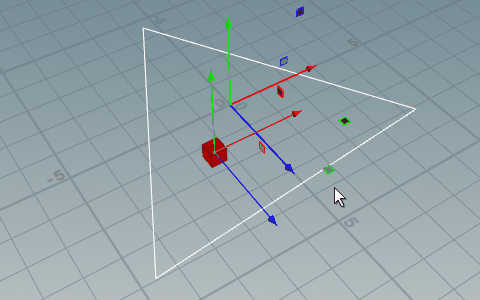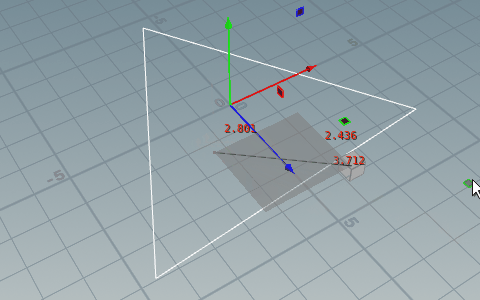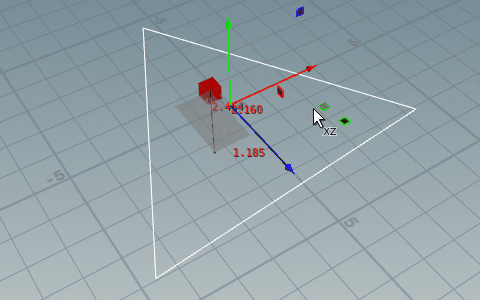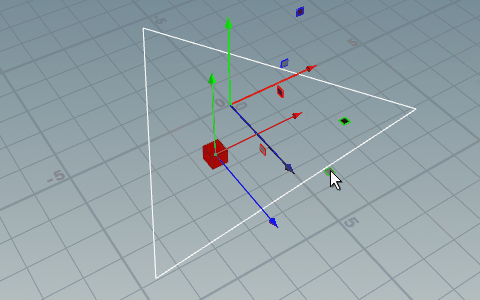
ポイントがプリミティブに内包されているか判定する
//
// 点がプリミティブ内に内包されているか判定する
// RunOver: Points
// input1: primitive
//
//
// 外積のY成分だけ返す関数
//
float crossY(vector v0; vector v1;)
{
return(v0.z * v1.x - v1.z * v0.x);
}
//
// 範囲のポリゴン内に入っているかチェック
//
int flag = 0;
for(int i = 0; i < nprimitives(1); i++)
{
// 三角形のポイント
int index[] = primpoints(1, i);
vector p0 = point(1, "P", index[0]);
vector p1 = point(1, "P", index[1]);
vector p2 = point(1, "P", index[2]);
float y0 = crossY(p1 - p0, @P - p0);
float y1 = crossY(p2 - p1, @P - p1);
float y2 = crossY(p0 - p2, @P - p2);
// 符号が一致(内側にある)
if((y0 > 0 && y1 > 0 && y2 > 0) || (y0 < 0 && y1 < 0 && y2 < 0))
{
flag = 1;
@Cd = set(1, 0, 0);
break;
}
}外積の符号が一致しているか確認する。一致していれば点は三角形の内側にある。
ちょうどエッジの上に乗っている場合も判定するするなら、不等号にイコールを入れる。
// 符号が一致(エッジも含む内側にある)
if((b1 >= 0 && b2 >= 0 && b3 >= 0) || (b1 <= 0 && b2 <= 0 && b3 <= 0))プリミティブがプリミティブに内包されているか判定する
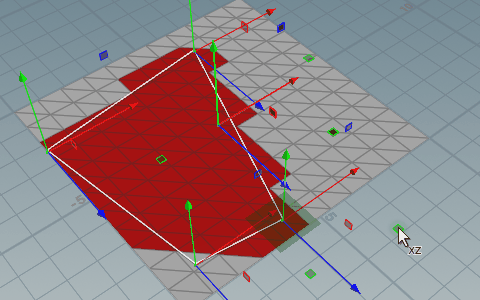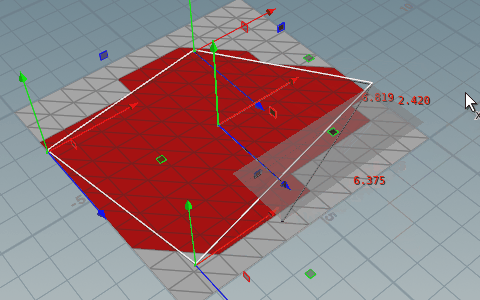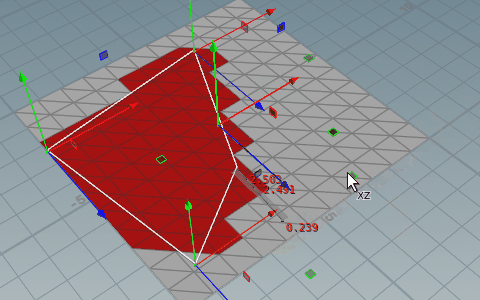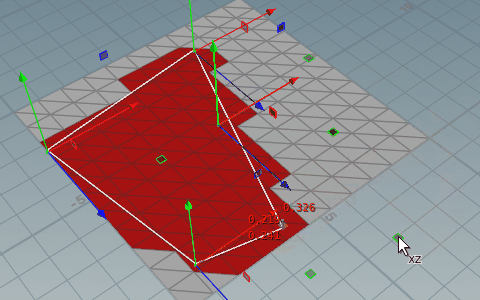
範囲用のポリゴンは必ず三角形に分割する。
// RunOver: Primitive
// input0: メッシュ
// input1: 範囲ポリゴン
// 外積で符号をチェックする
float cross2d(vector p1; vector p2; vector p3;)
{
return (p1.x - p3.x) * (p2.z - p3.z) - (p2.x - p3.x) * (p1.z - p3.z);
}
// 三角形のポイント
int pts[] = primpoints(0, @primnum);
int flags[];
for(int i = 0; i < len(pts); i++)
{
// 範囲のポリゴン内に入っているかチェック
for(int k = 0; k < nprimitives(1); k++)
{
// プリミティブのポイント
int index[] = primpoints(1, k);
vector v1 = point(1, "P", index[0]);
vector v2 = point(1, "P", index[1]);
vector v3 = point(1, "P", index[2]);
vector pos = point(0, "P", pts[i]);
float d1 = cross2d(pos, v1, v2);
float d2 = cross2d(pos, v2, v3);
float d3 = cross2d(pos, v3, v1);
// 符号が一致(内側にある)
if((d1 > 0 && d2 > 0 && d3 > 0) || (d1 < 0 && d2 < 0 && d3 < 0))
{
flags[i] = 1;
//setpointattrib(0, "Cd", pts[i], set(1,0,0));
break;
}
}
}
// 三角形内のポイントがひとつも内側にない場合
if(flags[0] == 0 && flags[1] == 0 && flags[2] == 0)
{
//removeprim(0, @primnum, 1);
}
else
{
i@group_flag = 1;
@Cd = set(1, 0, 0);
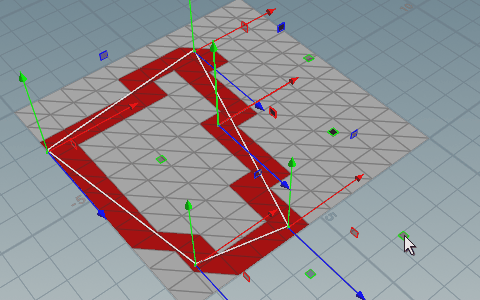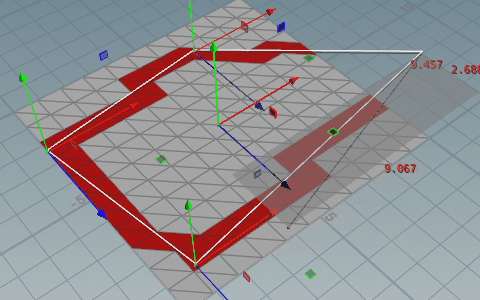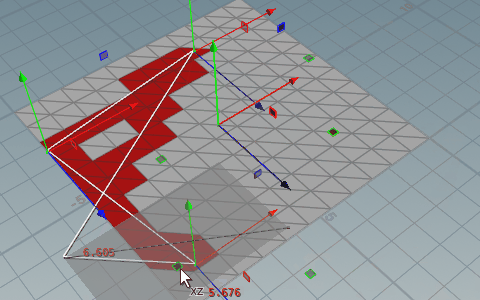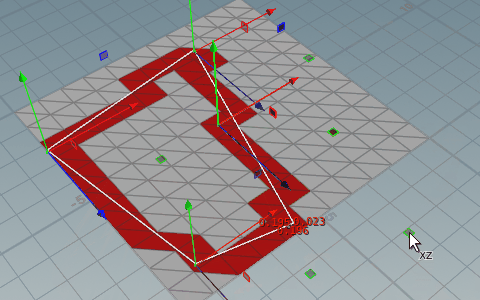
}エッジがプリミティブと交差しているか判定する
上記の内外判定はエッジ部分を含まなかったのでさらにVEXを追加することで補完することができる。
//
// コリジョンのラインとエッジが交差しているか判定する
// Run Over: Primitives
// input0: メッシュ
// input1: 範囲ポリゴン
//
//
// 線分が交差しているかチェックする関数
//
int IsIntersectLine(vector p0; vector p1; vector p2; vector p3)
{
int result = 0;
// まずは線分ABが直線CDと交差しているか判定
float ta = (p3.x - p2.x) * (p2.z - p0.z) + (p3.z - p2.z) * (p0.x - p2.x);
float tb = (p3.x - p2.x) * (p2.z - p1.z) + (p3.z - p2.z) * (p1.x - p2.x);
if(ta * tb < 0)
{
// 線分CDが直線ABと交差しているか判定
float tc = (p1.x - p0.x) * (p0.z - p2.z) + (p1.z - p0.z) * (p2.x - p0.x);
float td = (p1.x - p0.x) * (p0.z - p3.z) + (p1.z - p0.z) * (p3.x - p0.x);
if(tc * td < 0)
{
result = 1;
}
}
return result;
}
//
// メイン処理
//
// 三角形のポイント
int pts[] = primpoints(0, @primnum);
for(int i = 0; i < len(pts); i++)
{
vector v1 = point(0, "P", pts[i]);
vector v2 = point(0, "P", pts[i+1]);
// 最後のエッジ
if(i >= len(pts)-1)
{
v1 = point(0, "P", pts[i]);
v2 = point(0, "P", pts[0]);
}
// コリジョンのプリミティブごと
for(int j = 0; j < nprimitives(1); j++)
{
int pts2[] = primpoints(1, j);
// コリジョンプリミティブのラインごと
for(int k = 0; k < len(pts2); k++)
{
vector v3 = point(1, "P", pts2[k]);
vector v4 = point(1, "P", pts2[k+1]);
// 最後のエッジ
if(k >= len(pts2)-1)
{
v3 = point(1, "P", pts2[k]);
v4 = point(1, "P", pts2[0]);
}
if(IsIntersectLine(v1, v2, v3, v4) == 1)
{
setprimattrib(0, "Cd", @primnum, set(1, 0, 0));
i@group_flag = 1;
break;
}
}
}
}関連する記事