山岳地形向け経路探索のためのグラフ作成のアイデアとその手法です。もっともらしい経路探索の結果のためには元となるグラフの構造が重要になります。
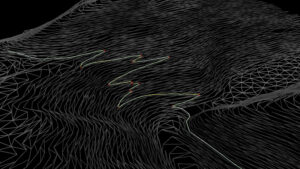
地形メッシュをグラフとして利用する
まずはもともとのメッシュを加工してグラフをつくってみます。

ハイトフィールドをConvert Height SOPを使いメッシュ化。

PolyReduce Sopを使いメッシュをリダクションし、さらにConvertline SOPでポリラインに変換する。各ポリラインにはこのようなコードを書いて勾配コストの計算をした。
//
// 勾配コストの計算
// RunOver:Primitives
//
// 最大勾配(%)
float maxSlope = 15;
float power = 2.0; // この値を大きくするほど、大きい値がさらに大きくなる
float scale = 100; // 他の要素(距離など)に対するスケール(重み)
int pts[] = primpoints(0, @primnum);
vector p0 = point(0, "P", pts[0]);
vector p1 = point(0, "P", pts[1]);
vector diff = normalize(p1 - p0);
float h = length(set(diff.x, 0, diff.z));
float slope = abs(diff.y / h); // 勾配(0-1)
f@slope = slope;
// 目安となる最大勾配以上には巨大な数字(ペナルティ)を掛ける
if(slope > maxSlope * 0.01)
slope *= 100;
f@slopeCost = pow(slope * scale, power);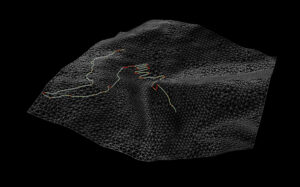
FindShortestPath SOPを使って2点間のパスを生成した結果。Primitive Cost AttributeにはslopeCostを設定した。急勾配の場所ではもう少し緩やかな経路を通って欲しいが、リダクションしたメッシュではそもそもそのようなルートがトポロジーの段階で用意されていない。
Scatter SOPで散布したポイントグラフをつないでグラフを作成する
緩やかなルートをグラフの段階で持ちたいので、グラフを生成する方向で考える。

Scatter SOPでメッシュ上にポイントを散布する。

ポイント同士をつなぐ。無数のポリラインが作成される。
//
// ポイント同士をつなぐ
// Run Over: Points
//
// 長さ(m)の閾値
float lengthThreshold = 100;
// 勾配(%)の閾値
float angleThreshold = 0.25;
// 範囲内のポイントを探す
int npt[] = nearpoints(0, @P, lengthThreshold);
for(int i = 0; i < len(npt); i++)
{
if(npt[i] > @ptnum)
{
vector p0 = @P;
vector p1 = point(0, "P", npt[i]);
vector diff = normalize(p1 - p0);
float L = length(set(diff.x, 0, diff.z));
float slope = abs(diff.y / L); // 勾配(0-1)
if(slope < angleThreshold)
{
if(L < pow(lengthThreshold,2))
{
int prim = addprim(0, "polyline");
addvertex(0, prim, @ptnum);
addvertex(0, prim, npt[i]);
}
}
}
}重複しているポリラインがたくさん出来るため、削除する必要がある。

XZ平面から見て交差するポリラインを探し、勾配の緩いほうを残す。
//
// ポリラインがXZ平面上で交差していたら一方を削除する
// Run Over: Primitives
//
// 線分が交差しているかチェックする関数
int IsIntersectLine(vector p0; vector p1; vector p2; vector p3)
{
int result = 0;
// まずは線分ABが直線CDと交差しているか判定
float ta = (p3.x - p2.x) * (p2.z - p0.z) + (p3.z - p2.z) * (p0.x - p2.x);
float tb = (p3.x - p2.x) * (p2.z - p1.z) + (p3.z - p2.z) * (p1.x - p2.x);
if(ta * tb < 0)
{
// 線分CDが直線ABと交差しているか判定
float tc = (p1.x - p0.x) * (p0.z - p2.z) + (p1.z - p0.z) * (p2.x - p0.x);
float td = (p1.x - p0.x) * (p0.z - p3.z) + (p1.z - p0.z) * (p3.x - p0.x);
if(tc * td < 0)
{
result = 1;
}
}
return result;
}
//
// ポリラインが交差していたら勾配の緩い方を削除する
//
int pts[] = primpoints(0, @primnum);
vector p0 = point(0, "P", pts[0]);
vector p1 = point(0, "P", pts[-1]);
for(int i = 0; i < nprimitives(0); i++)
{
if(i != @primnum)
{
int pts2[] = primpoints(0, i);
vector p2 = point(0, "P", pts2[0]);
vector p3 = point(0, "P", pts2[-1]);
vector cross;
if(IsIntersectLine(p0, p1, p2, p3))
{
float slope = prim(0, "slope", i);
float cost0 = length(p1-p0) + pow(f@slope, 2) * 10000;
float cost1 = length(p3-p2) + pow(slope,2) * 10000;
if(cost0 > cost1)
{
removeprim(0, @primnum, 1);
break;
}
}
}
}線分同士の交差判定の解説はこちら
線分の交差判定と交点の求め方

FindshortestPath SOPでパスを生成した結果。勾配に沿って緩やかな経路を取れるグラフ構造になった。
高さ方向のトポロジーの密度を高くする
急勾配ほどポイントのY軸方向の間隔を狭めたいのでポイントの散布前にメッシュをY軸方向に引き伸ばす。

メッシュを縦方向にn倍伸ばし

Scatter SOPでポイントを散布する。

そして1/n倍して元のスケールへ戻す。

このポイントを同じように結び、勾配の緩いものだけを残すと、縦方向に圧縮されたトポロジーができる。
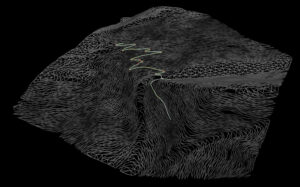
斜面をちょうどよい勾配で通るパスが作成できているのでは。さらによさそうな方法を思いついたら追記していきます。


