ベジェ曲線の特徴
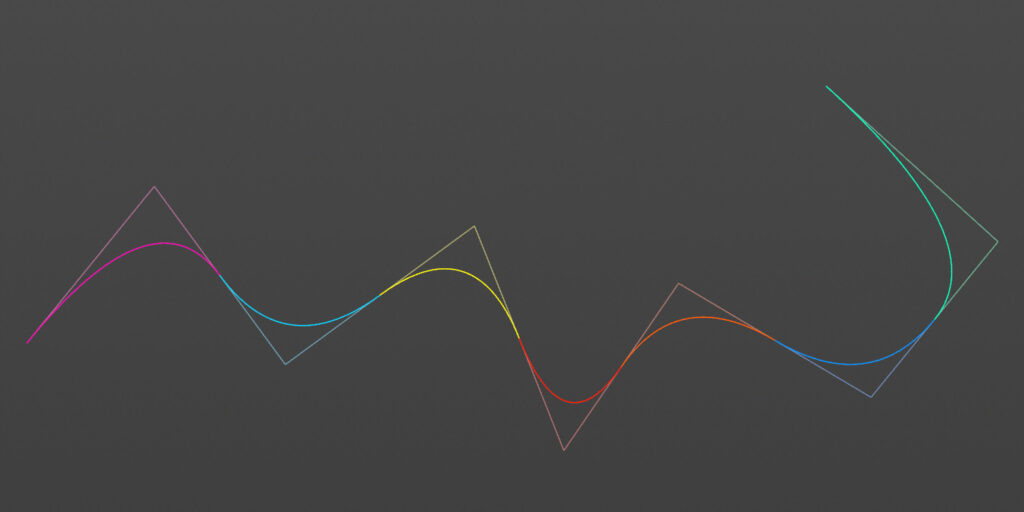
・ベジェ曲線は制御点によって定義される
・曲線は必ず制御点の内側に描画される
制御点の線形補完を繰り返すことで滑らかな曲線を生成します。
1次のベジェ曲線
P = (1-t)P0 + tP1
1次のベジェ曲線は一本の直線です。
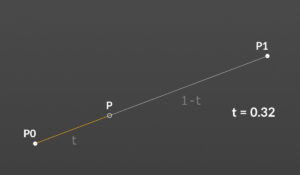
tはパラメトリック座標で、0-1の範囲の値。線分上をどれだけの割合を進んだかを表す数値。点Pは、t=0の時はP0で、t=1の時にP1に到達します。tが0から1まで実行されることで直線が形成されます。これを基本として曲線へ発展させていきます。
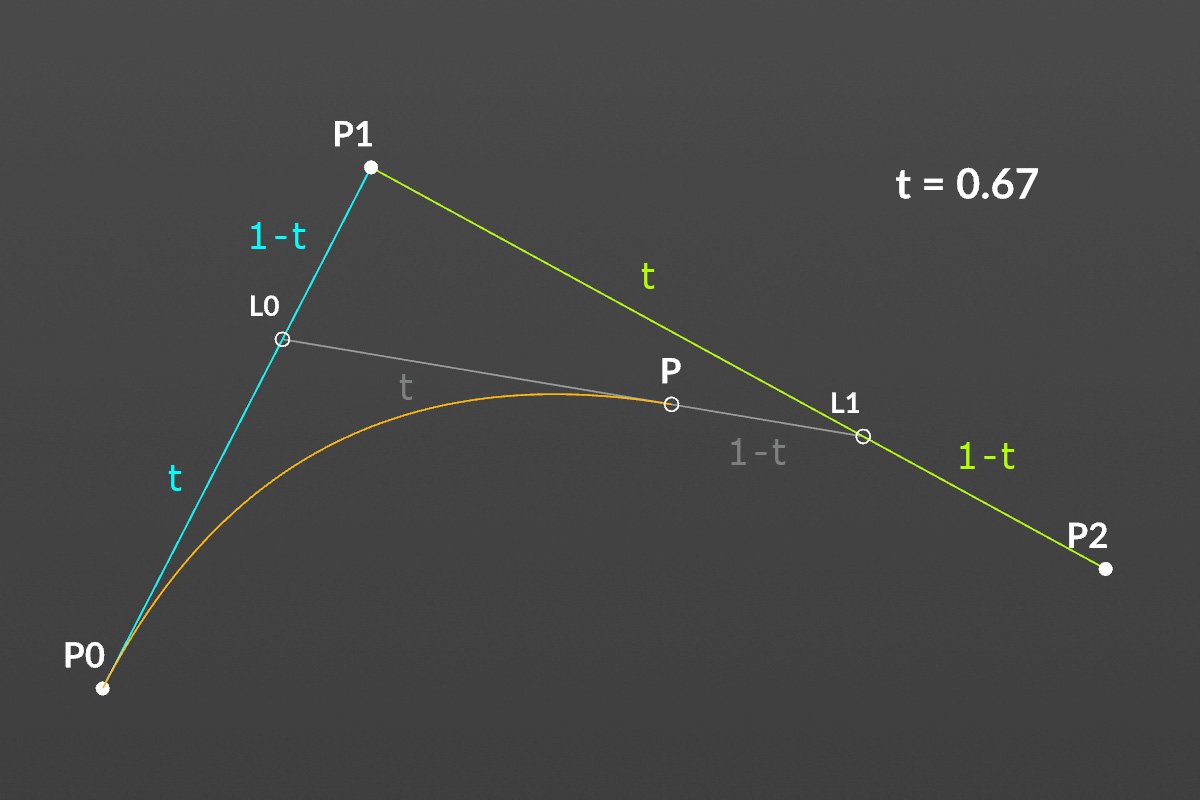
2次のベジェ曲線
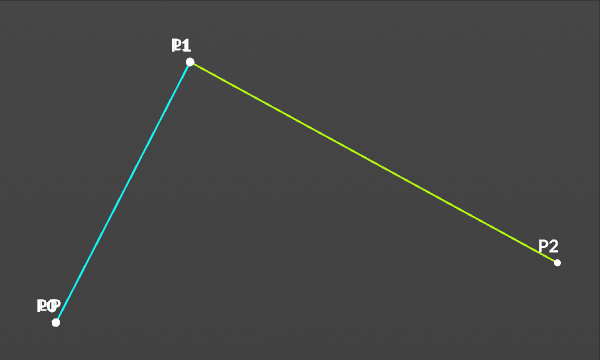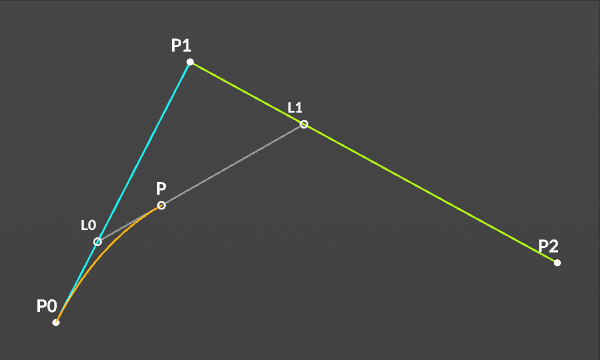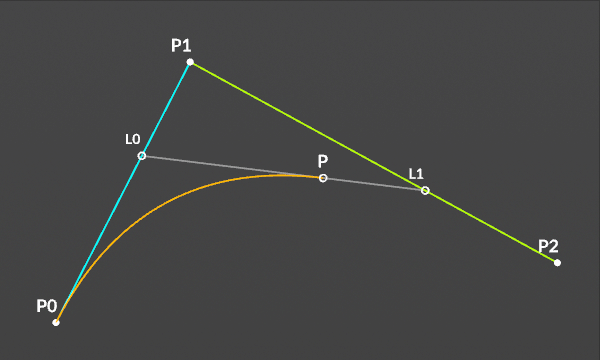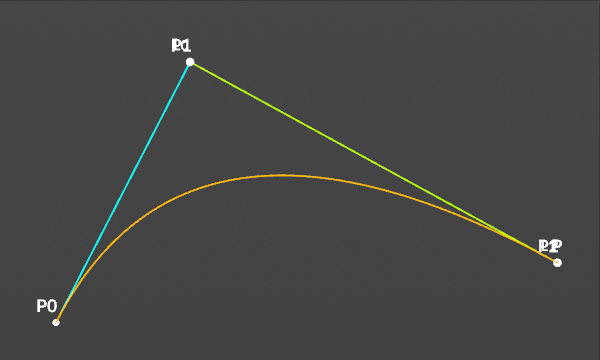
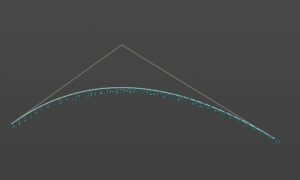
2次のベジェ曲線は３つの制御点で描画される。
計算式
P = (1-t)2P0+2(1-t)tP1 + t2P2
点Pは、t=0の時はP0で、t=1の時にP2になります。tが0から1まで実行されることで曲線が形成されます。
以下、式の解説です。
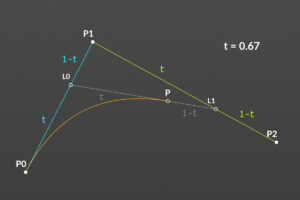
2点間のポイントの座標
L0 = (1-t)P0 + tP1
L1 = (1-t)P1 + tP2
P = (1-t)L0 + tL1
なので、L0とL1に式を代入すると
P = (1-t)2P0+2(1-t)tP1 + t2P2
となります。
コードで描画
//
// 2次（Quandric）のベジェ曲線
//
// input1に3点のポリラインをつなげる
// Run Over: Detail
//
int pts[] = primpoints(1, 0);
vector p0 = point(1, "P", pts[0]);
vector p1 = point(1, "P", pts[1]);
vector p2 = point(1, "P", pts[2]);
//
// ベジェ曲線を描く
//
int prim = addprim(0, "polyline");
int num = 40; // サンプルポイント数
for(int i = 0; i < num; i++)
{
float t = i / float(num-1);
vector pos = (1-t)*(1-t)*p0 + 2*(1-t)*t*p1 + t*t*p2;
int pt = addpoint(0, pos);
addvertex(0, prim, pt);
}3次のベジェ曲線
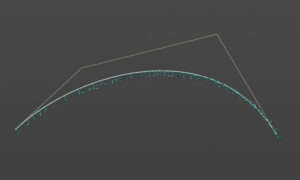
3次のベジェ曲線は4つの制御点で描画される。
計算式
P = (1-t)3P0+3(1-t)2tP1 + 3(1-t)t2P2 + t3P3
少し複雑になっていますが、やっていることは2次のベジェ曲線と同じです。
L0 = (1-t)P0 + tP1
L1 = (1-t)P1 + tP2
L2 = (1-t)P2 + tP3
S0 = (1-t)L0 + tL1
S1 = (1-t)L1 + tL2
L0とL1に式を代入する
S0 = (1-t)2P0+2(1-t)tP1 + t2P2
S1 = (1-t)2P1+2(1-t)tP2 + t2P3
P = (1-t)S0 + tS1
S0とS1に代入すると
P = (1-t)3P0+3(1-t)2tP1 + 3(1-t)t2P2 + t3P3
となります。
コードで描画
//
// 3次（Cubic）のベジェ曲線
//
// input1に4点のポリラインをつなげる
// Run Over: Detail
//
int pts[] = primpoints(1, 0);
vector p0 = point(1, "P", pts[0]);
vector p1 = point(1, "P", pts[1]);
vector p2 = point(1, "P", pts[2]);
vector p3 = point(1, "P", pts[3]);
//
// ベジェ曲線を描く
//
int prim = addprim(0, "polyline");
int num = 40; // サンプルポイント数
for(int i = 0; i < num; i++)
{
float t = i / float(num-1);
vector pos = (1-t)*(1-t)*(1-t)*p0 + 3*(1-t)*(1-t)*t*p1 + 3*(1-t)*t*t*p2 + t*t*t*p3;
int pt = addpoint(0, pos);
addvertex(0, prim, pt);
}連続性のあるベジェ曲線を描画する方法は以下のページに書きました。
ベジェ曲線の描画
