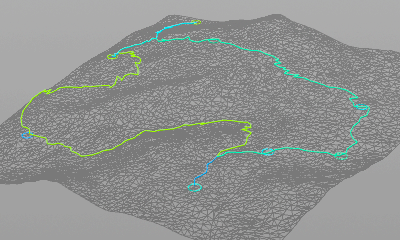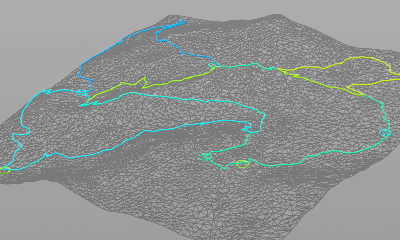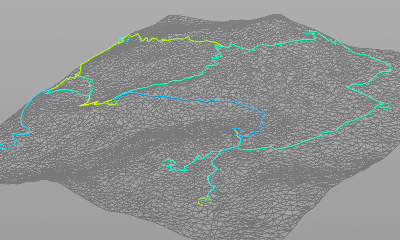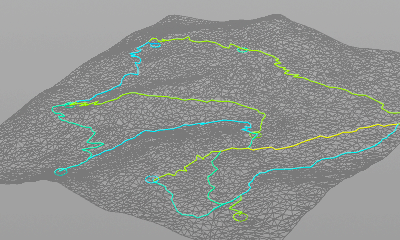
地形メッシュ上に集落のポイントを置き、それらをつないだ道路のネットワークを生成します。「集落と街道の生成」という論文を参考にしました。
アルゴリズムの流れ
集落をノード、道をリンクとしたネットワークモデルとして考える。
集落ポイントを配置する
まずはベースとなる地形のメッシュを用意します。
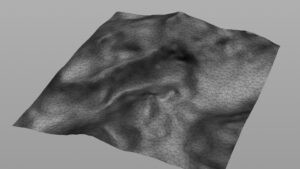
Normal SOPでメッシュの角度を@Nに設定した後にWrangle SOPで分布マップをつくる

勾配の緩やかな場所にScatter SOPでポイントを配置した。
//
// 地形メッシュの勾配マップをつくる
// Run Over: Points
//
vector up = set(0, 1, 0);
float angle = acos(dot(@N, up)); // Y軸との角度差を角度で求める
angle /= (PI / 2); // 90°でスケールする
// Scatter SOPの分布で使う
f@density = pow(1-angle, 8); // n乗して平地部分を狭める
// 色で視覚化
@Cd = f@density;集落同士をポリラインで結ぶ
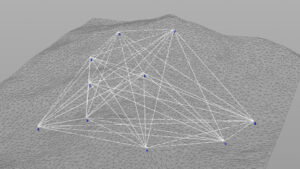
すべてのポイント同士をポリラインでつないでから
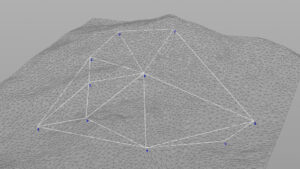
交差しているポリラインの長い方を削除していく。
//
// ポイント同士をポリラインでつなぐ
// Run Over: Points
//
for(int i = 0; i < npoints(0); i++)
{
if(i > @ptnum)
{
{
int prim = addprim(0, "polyline");
addvertex(0, prim, @ptnum);
addvertex(0, prim, i);
}
}
}//
// ポリラインがXZ平面上で交差していたら長い方を削除する
// Run Over: Primitives
//
// 線分が交差しているかチェックする関数
int IsIntersectLine(vector p0; vector p1; vector p2; vector p3)
{
int result = 0;
// まずは線分ABが直線CDと交差しているか判定
float ta = (p3.x - p2.x) * (p2.z - p0.z) + (p3.z - p2.z) * (p0.x - p2.x);
float tb = (p3.x - p2.x) * (p2.z - p1.z) + (p3.z - p2.z) * (p1.x - p2.x);
if(ta * tb < 0)
{
// 線分CDが直線ABと交差しているか判定
float tc = (p1.x - p0.x) * (p0.z - p2.z) + (p1.z - p0.z) * (p2.x - p0.x);
float td = (p1.x - p0.x) * (p0.z - p3.z) + (p1.z - p0.z) * (p3.x - p0.x);
if(tc * td < 0)
{
result = 1;
}
}
return result;
}
//
// ポリラインが交差している場合、相手より自分のほうが長かったら削除する
//
int pts[] = primpoints(0, @primnum);
vector p0 = point(0, "P", pts[0]);
vector p1 = point(0, "P", pts[-1]);
for(int i = 0; i < nprimitives(0); i++)
{
int pts2[] = primpoints(0, i);
vector p2 = point(0, "P", pts2[0]);
vector p3 = point(0, "P", pts2[-1]);
vector cross;
if(IsIntersectLine(p0, p1, p2, p3))
{
if(length2(p1-p0) > length2(p3-p2))
{
removeprim(0, @primnum, 1);
break;
}
}
}FindShortestPath SOPで道に変形する

コリジョンメッシュにConvertline SOPを使ってポリライン化(グラフ化)する。ポリラインごとに勾配を設定しておく。FindShortestPath SOPでポリラインの始点と終点を使ってその間のパスを生成し置き換える。(重複する場所も出てくるのでPolypath SOPで整理するのもいいかも)

各ノードについて隣接ノード数を計算する。すべてのポイントから各上位ノードまで経路探索を行う。ダイクストラ法を使ってコストが最小となる経路を計算して、通ったリンクに回数を記録していく。

リンクの使用回数を視覚化した画像。黄色いほど回数が多く、青いところほど使われていない。

使われていない道を削除したもの。
道のコスト計算
始点標高he、リンク総長le、間の各セグメントの標高と長さをhi、liとして、次の式によって計算する。
\(c=l_e^{2}+\sum_{i=0}^{n} l_i(h_e-h_i)\)
第一項 \(l_e^{2}\)
リンク全体の長さの2乗は、道が長くなるほどコストが急激に増えるペナルティを与えている。
第二項 \(\sum_{i=0}^{n} l_i(h_e-h_i)\)
標高差に通過距離をかけて積算する。どれだけ標高変化を伴うかを評価しており、始点から見てなるべく平坦な道がコストが低くなる設計になっている。

奥の2本は水平距離と始点と終点の高さも同じだが、勾配に違いがある。緩やかな方がコストが低い。手前のラインは奥の2本に比べて長いのでコストが高くなっている。
VEXのコード
//
// ポリラインの勾配コストを計算する
// 目的地まで短く、かつ経路中の工程が少ない道がよく利用されると想定する。
// Run Over: Primitives
//
// 2点間の水平距離を計算する
float horizontalDistance(vector p0; vector p1)
{
vector d = p1 - p0;
return length(set(d.x, 0, d.z));
}
int pts[] = primpoints(0, @primnum);
vector start = point(0, "P", pts[0]);
float sum_height = 0;
float sum_length = 0;
for(int i = 0; i < len(pts)-1; i++)
{
vector p0 = point(0, "P", pts[i]);
vector p1 = point(0, "P", pts[i+1]);
float L = horizontalDistance(p0, p1);
sum_height += L * abs(p1.y - start.y);
sum_length += L;
}
f@cost = pow(sum_length, 2) + sum_height;ダイクストラの経路探索
関数化したダイクストラ法を使い、ポイント同士を総当たりで経路探索するようにしたコード。Python SOPを使う。

各リンクに通った回数が加算される。
各ポイントには事前に配列を用意する。それぞれ対になるように順に並べる。
connectedPrim[]:隣接するポリライン
connectedPoint[]:隣接するポイント(ポリラインの反対側にある次のポイント)
distance[]:コストを記録した配列
#
# 次数の小さいノードから大きいノードへ経路探索し、結果を累積する
#
node = hou.pwd()
geo = node.geometry()
import time
import copy
# Start
start_time = time.time()
# 地点クラス
class Node:
def __init__(self, connectedPoint, connectedPrim, dist, position):
# インデックス
self.index = -1
# 直前のインデックス
self.prevPt = -1
# フラグ
self.flag = 0
# コスト(一応大きな数を入れておく)
self.totalCost = 10e9
# 接続するPoint
self.connectedPoint = connectedPoint
# 接続するPrim
self.connectedPrim = connectedPrim
# 道路のコスト(距離)
self.dist = dist
# 座標
self.position = position
# それまでのコスト
self.score = 0
#
# Dykstraの経路探索の関数
#
def pathFinding(start, goal, node):
# startからのルートをリストに入れる
node[start].totalCost = 0.0
node[start].prevPt = start
node[start].flag = 1
# ルートリスト
openList = []
openList.append(start)
count = 0
# リストが空になるまで続ける
while len(openList) > 0:
count += 1
if count > 1000:
print ("loop error")
break
# コストの低いものを取得してリストから削除する
currentPt = openList.pop(0)
for i in range(len(node[currentPt].connectedPoint)):
nextPt = node[currentPt].connectedPoint[i]
# 距離のコスト
cost = node[currentPt].totalCost + node[currentPt].dist[i]
# もし探索済みで、新しいルートのほうがコストが低い場合は更新する
if node[nextPt].flag == 1:
if cost < node[nextPt].totalCost:
node[nextPt].totalCost = cost
node[nextPt].prevPt = currentPt
openList.append(nextPt)
else:
node[nextPt].totalCost = cost
node[nextPt].prevPt = currentPt
node[nextPt].flag = 1
# ゴールの地点なら次の地点は探索しない
if nextPt != goal:
openList.append(nextPt)
else:
continue
break
# ルートを検索
routePoint = []
routePrim = []
if node[goal].prevPt != -1:
count = 0
pt = goal
while(pt != start):
routePoint.append(pt)
pt = node[pt].prevPt
count += 1
if count > 100:
break
# ルートポイント
routePoint.append(start)
routePoint.reverse()
else:
pass
#print 'No Route Found.'
# ポイントをたどってポリラインのリストをつくる
for i in range(len(routePoint)-1):
# 重複を考慮する
link = []
for j in range(len(node[routePoint[i]].connectedPoint)):
if node[routePoint[i]].connectedPoint[j] == routePoint[i+1]:
link.append(j)
# コストの低いルートを選ぶ
closeIndex = -1
minDist = 10e9
for j in range(len(link)):
if node[routePoint[i]].dist[link[j]] < minDist:
minDist = node[routePoint[i]].dist[link[j]]
closeIndex = link[j]
routePrim.append(node[routePoint[i]].connectedPrim[closeIndex])
return routePoint, routePrim
# 分岐するルートと距離の情報を格納する
connectedPoint = []
connectedPrim = []
dist = []
position = []
for pt in geo.points():
connectedPoint.append(pt.intListAttribValue("connectedPoint"))
connectedPrim.append(pt.intListAttribValue("connectedPolyline"))
dist.append(pt.floatListAttribValue("distance"))
position.append(pt.position())
# ノードクラスのリストを初期化して値を格納
nodes = []
for i in range(len(geo.points())):
nodes.append(Node(connectedPoint[i], connectedPrim[i], dist[i], position[i]))
nodes[i].index = i
# 結果の優先度リストの作成
route_score = []
for i in range(len(geo.prims())):
route_score.append(0)
# 次数のリストを取得
route_degree = []
for pt in geo.points():
route_degree.append(pt.intAttribValue("degree"))
# ポイントにCdアトリビュートを作成する
geo.addArrayAttrib(hou.attribType.Prim, "routePoint", hou.attribData.Int)
geo.addArrayAttrib(hou.attribType.Prim, "routePrim", hou.attribData.Int)
#
# 自分の次数より上のゴールに対して総当たりで経路探索する
#
count = 0
for i in range(len(geo.points())):
for j in range(len(geo.points())):
if i != j and route_degree[i] < route_degree[j]:
#print str(i) + "," + str(j)
start_pt = i
goal_pt = j
nodes_copy = copy.deepcopy(nodes)
routePoint, routePrim = pathFinding(start_pt, goal_pt, nodes_copy)
#print route
# ポイントのリストに結果を加算する
for k in range(len(routePrim)):
route_score[routePrim[k]] += 1
count += 1
prim = geo.createPolygon()
prim.setAttribValue('routePoint', routePoint)
prim.setAttribValue('routePrim', routePrim)
#print("count: " + str(count))
geo.addArrayAttrib(hou.attribType.Global, 'priority', hou.attribData.Int, 1)
geo.setGlobalAttribValue('priority', route_score)
# End
elapsed_time = time.time() - start_time
#print ("Dykstra_route::time:{0}".format(elapsed_time) + "[sec]")
