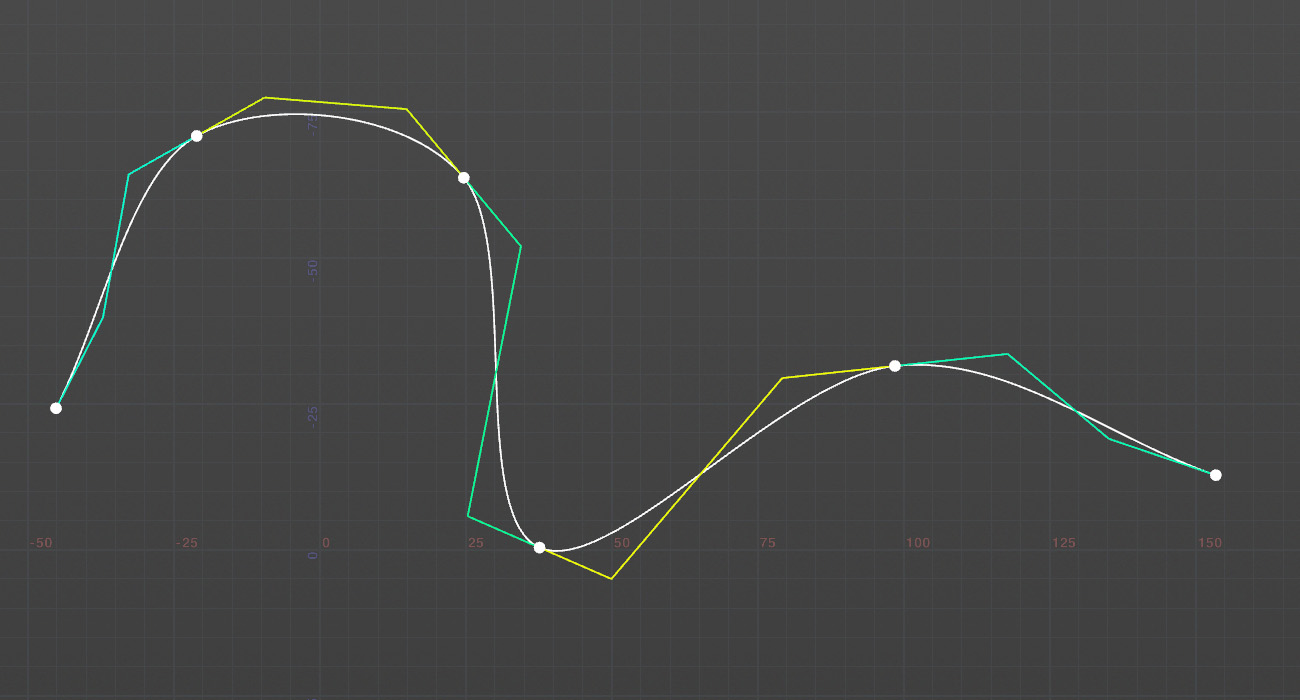
Catmull-Romスプラインをベジェ曲線に変換する

Catmull-Romスプラインの接線ベクトルを使うことで3次ベジェ曲線の制御点を生成することができる。
Catmull-Romスプライン曲線

計算式
コード

計算式

Catmull-Romスプラインの接線ベクトル\(V_0\)、\(V_1\)を利用する。

3次ベジェ曲線の定義は
\(P = (1-t)^3P_0+3(1-t)^2tP_1+3(1-t)t^2P_2+t^3P_3\)

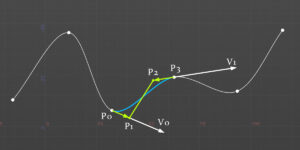
制御点はそれぞれ
\(P_0\)=始点
\(P_3\)=終点
\(P_1 = P_0+\frac{1}{3}V_0\)
\(P_2 = P_3-\frac{1}{3}V_1\)

Catmull-Romスプラインの接線ベクトル（速度）に\(\frac{1}{3}\)を掛けると制御点になる。ベジェ曲線の1階微分を求めると3倍の係数がでるため、1/3にスケールダウンすることで整合が取れる。

コード

Catmull-Romスプラインを描画するコードに追加する形で制御点のポリラインを生成している。

//
// Cutmul-Rom曲線とベジェ制御点を描く
// Run Over: Detail
//
for(int i = 0; i < npoints(0)-1; i++)
{
    vector p0 = point(0, "P", i-1);
    vector p1 = point(0, "P", i);
    vector p2 = point(0, "P", i+1);
    vector p3 = point(0, "P", i+2);
    
    // 始点の速度ベクトル
    vector v0;
    if(i > 0)
        v0 = (p2 - p0) / 2;
    else // 始点
        v0 = (p2 - p1);
        
    // 終点の速度ベクトル
    vector v1;
    if(i < npoints(0)-2)
        v1 = (p3 - p1) / 2;
    else // 終点
        v1 = p2 - p1;
    
    // p1-p2間でカーブを描く
    int prim = addprim(0, "polyline");
    int num = 100;
    for(int j = 0; j < num; j++)
    {
        float t = j / float(num-1);
        vector pos = (-2*(p2-p1)+v1+v0)*t*t*t + (3*(p2-p1)-v1-2*v0)*t*t + v0*t + p1;
        
        int pt = addpoint(0, pos);
        addvertex(0, prim, pt);
    }
    
    // 制御点
    prim = addprim(0, "polyline");
    
    vector c0 = p1;
    int pt = addpoint(0, c0);
    addvertex(0, prim, pt);
    
    vector c1 = p1 + v0 / 3;
    pt = addpoint(0, c1);
    addvertex(0, prim, pt);
    
    vector c2 = p2 - v1 / 3;
    pt = addpoint(0, c2);
    addvertex(0, prim, pt);
    
    vector c3 = p2;
    pt = addpoint(0, c3);
    addvertex(0, prim, pt);
    
    setprimgroup(0, "guide", prim, 1);
}