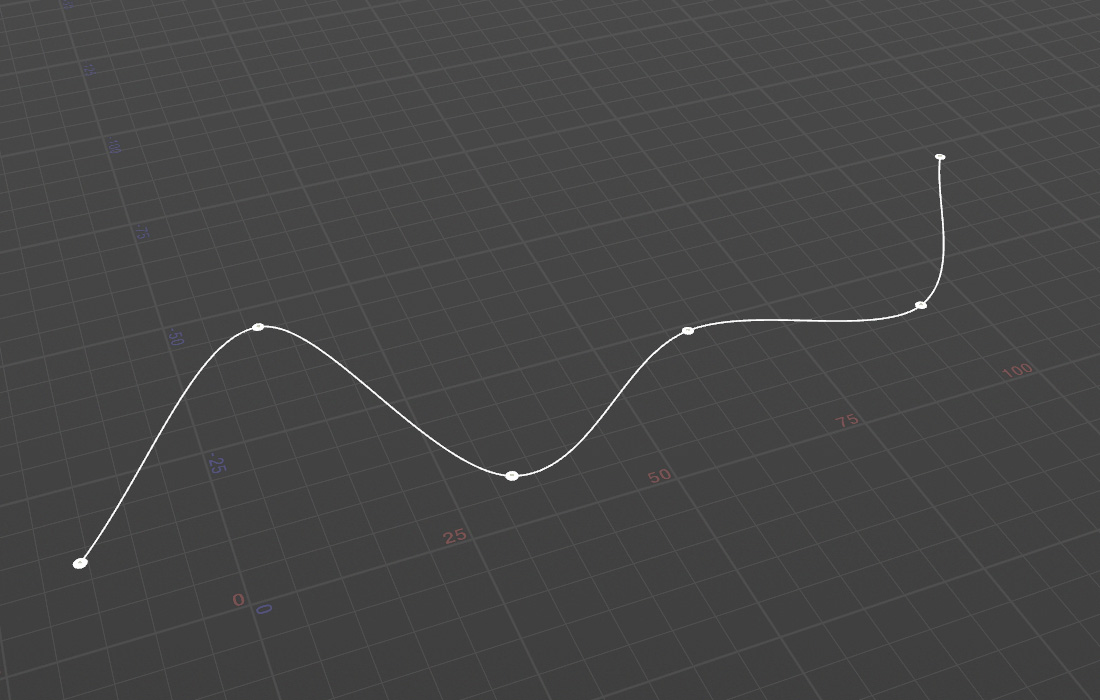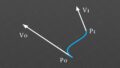
Catmull-Romスプライン曲線

Catmull-Romスプライン曲線は制御点をすべて通るような曲線を引くアルゴリズム。エルミート曲線を連続するようにつなぎあわせている。エルミート曲線

エルミート曲線の始点ベクトルと終点ベクトルはそれぞれ前の制御点と次の制御点を結んだラインをベクトルにする。

処理の流れ
コード

処理の流れ

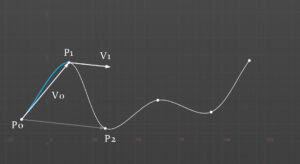
最初のポイントはP₀からP₁へのベクトルを始点ベクトルする。終点のベクトルはP₀からP₂への半分の長さのベクトルを使って、P₀からP₁へエルミート曲線を描く。

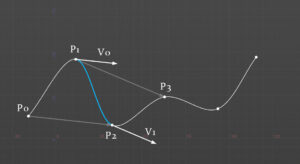
中間のポイントはP₀からP₂へのベクトルの半分の長さを始点ベクトル、P₁からP₃へのベクトルの半分の長さを終点ベクトルとして、P₁からP₂へエルミート曲線を描く。

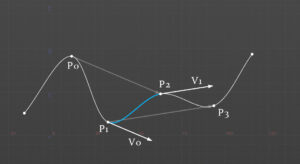
次のポイントの始点ベクトルは前回の終点ベクトルと一致する。これで連続性が保たれている。

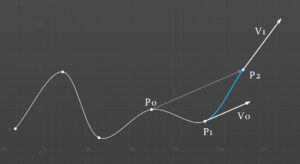
最後のポイントはP₀からP₂への半分の長さのベクトルを始点ベクトルする。終点のベクトルはP₁からP₂へのベクトルを使って、P₁からP₂へエルミート曲線を描く。

コード

//
// Cutmul-Rom曲線を描く
// Run Over: Detail
//
for(int i = 0; i < npoints(0)-1; i++)
{
    vector p0 = point(0, "P", i-1);
    vector p1 = point(0, "P", i);
    vector p2 = point(0, "P", i+1);
    vector p3 = point(0, "P", i+2);
    
    // 始点の速度ベクトル
    vector v0;
    if(i > 0)
        v0 = (p2 - p0) / 2;
    else // 始点
        v0 = (p2 - p1);
        
    // 終点の速度ベクトル
    vector v1;
    if(i < npoints(0)-2)
        v1 = (p3 - p1) / 2;
    else // 終点
        v1 = p2 - p1;
    
    // p1-p2間でエルミート曲線を描く
    int prim = addprim(0, "polyline");
    int num = 100;
    for(int j = 0; j < num; j++)
    {
        float t = j / float(num-1);
        vector pos = (-2*(p2-p1)+v1+v0)*t*t*t + (3*(p2-p1)-v1-2*v0)*t*t + v0*t + p1;
        
        int pt = addpoint(0, pos);
        addvertex(0, prim, pt);
    }
}