エルミート曲線

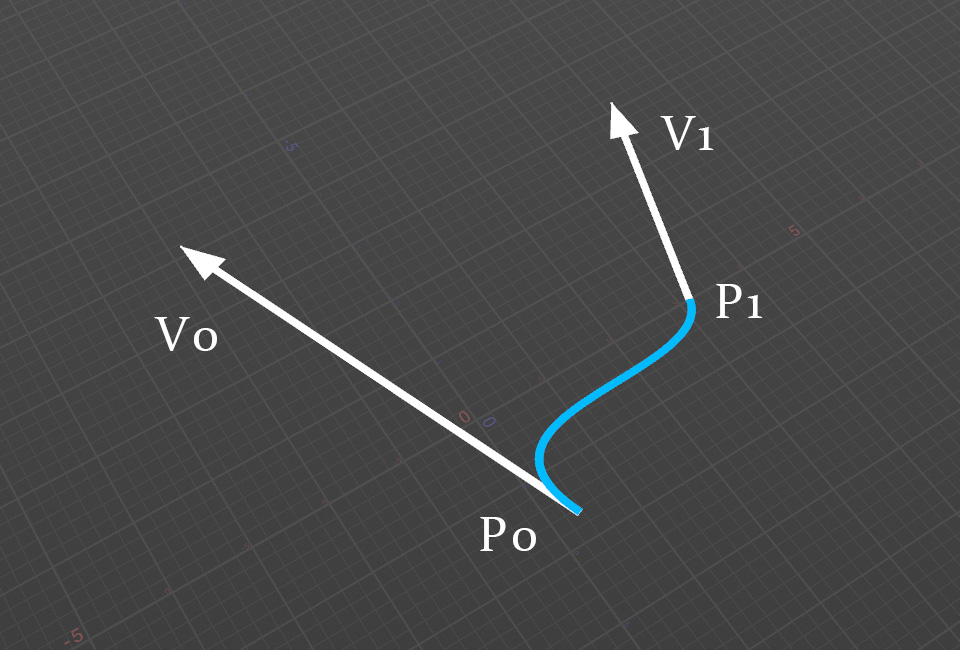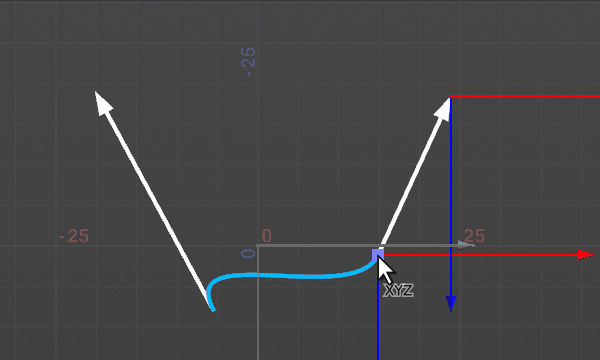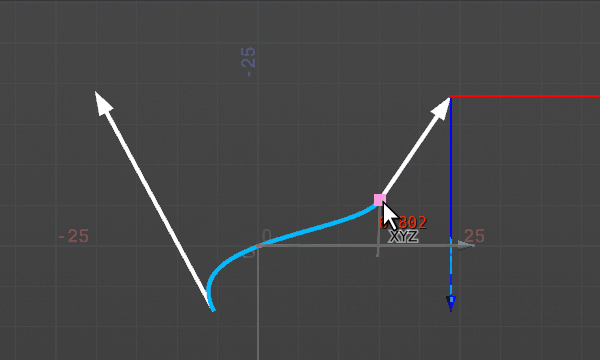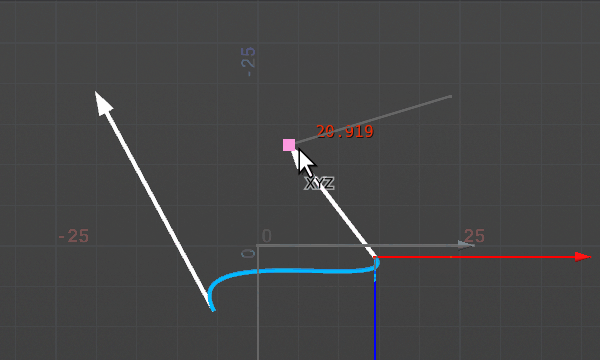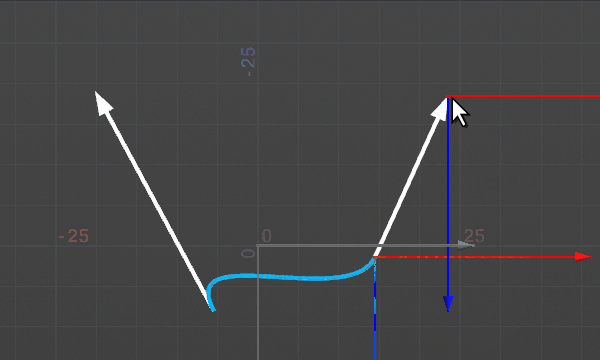
エルミート曲線は３次方程式を使い、位置だけでなく始点と終点の接線情報も考慮して間を補完する曲線を作ることができる。始点から始点のベクトル方向に飛び出した曲線が、終点では終点ベクトルの向きで到着する。3次方程式で表現されるため、始点からひとつめのカーブへ進み、ふたつめのカーブから終点へ進む、という形になる。

計算式

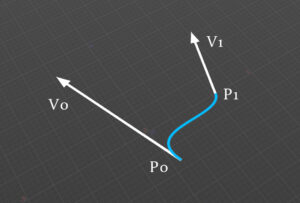
エルミート曲線のパラメータは

始点（P₀）
始点の速度ベクトル（V₀）
終点（P₁）
終点の速度ベクトル（V₁）

エルミート補完ではカーブの式を3次関数として定義する。

\(f(t) = at^3+bt^2+ct+d\)

\(f(t)\)は時間（t）に対する位置。tは０～１。

始点\(P_0 = f(0) = d\)・・・①

終点\(P_1 = f(1) = a + b + c +d\)・・・②

式を微分すると、

\(f'(t) = 3at^2+2bt+c\)

\(f'(t) \)は速度の関数（時間tに対する変化率）となる。（スカラー値ではなくベクトル）

始点のベクトル\(V_0 = f'(0) = c\)・・・③

終点のベクトル\(V_1 = f'(1) = 3a+2b+c\)・・・④

①と③を②に代入すると

\(P_1 = a + b + P_0 + V_0\)

③を④に代入すると

\(V_1 = 3a + 2b + V_0\)

a, bについて解くと

\(a = -2(P_0 – P_1) + V_0 + V_1\)

\(b = 3(P_1 – P_0) – 2V_0 – V_1\)

3次式\(f(t) = at^3+bt^2+ct+d\)に代入していくと

\(c = V_0\)、\(d= P_0\)なので

\(f(t) = (-2(P_0 – P_1) + V_0 + V_1)t^3+(3(P_1 – P_0) – 2V_0 – V_1)t^2+V_0t+P_0\)

となる。

コード

ポリライン２本をマージしたものをWrangleノードに差しています。

//
// エルミート曲線を描く
// Run Over: Detail
//
int pts[] = primpoints(0, 0);
int pts2[] = primpoints(0, 1);

vector p0 = point(0, "P", pts[0]);
vector p1 = point(0, "P", pts[1]);
vector p2 = point(0, "P", pts2[0]);
vector p3 = point(0, "P", pts2[1]);

vector v0 = (p1 - p0);
vector v1 = (p3 - p2);

int prim = addprim(0, "polyline");
int num = 100;
for(int i = 0; i < num; i++)
{
    float t = i / float(num-1);
    vector pos = (-2*(p2-p0)+v1+v0)*t*t*t + (3*(p2-p0)-v1-2*v0)*t*t + v0*t + p0;
    
    int pt = addpoint(0, pos);
    addvertex(0, prim, pt);
}