環境:Houdini 20.5.487

平面上でポリラインの各ポイントを幅が一定となるようにオフセットします。
処理の流れ
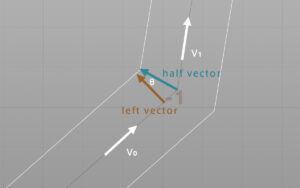
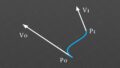
ポイントにおけるハーフベクトルはポリラインの進行方向のベクトルV0の逆ベクトルと続くV1を足したベクトルになる。レフトベクトルとハーフベクトルの成す角θはそれぞれを正規化したベクトルの内積から計算できる。長さはleft vector = 1とすると、half vector = 1 / cosθになる。各ポイントをこの長さでオフセットすれば幅が一定となる。
コード
始点、終点、中間点と場合分けする。
//
// ポリラインの幅を一定に維持してオフセットする
// Run Over: Primitives
//
// オフセット距離
float offset = 0.2;
// アップベクトル
vector up = set(0,1,0);
int pts[] = primpoints(0, @primnum);
for(int i = 0; i < len(pts); i++)
{
// 始点
if(i == 0)
{
vector p0 = point(0, "P", pts[i]);
vector p1 = point(0, "P", pts[i+1]);
vector v0 = normalize(p1-p0);
vector left = cross(up, v0);
vector new_pos = p0 + offset * normalize(left);
setpointattrib(0, "P", pts[i], new_pos);
}
// 終点
else if(i == len(pts)-1)
{
vector p0 = point(0, "P", pts[i-1]);
vector p1 = point(0, "P", pts[i]);
vector v0 = normalize(p1-p0);
vector left = cross(up, v0);
vector new_pos = p1 + offset * normalize(left);
setpointattrib(0, "P", pts[i], new_pos);
}
// 中間点
else
{
vector p0 = point(0, "P", pts[i-1]);
vector p1 = point(0, "P", pts[i]);
vector p2 = point(0, "P", pts[i+1]);
vector v0 = normalize(p1 - p0);
vector v1 = normalize(p2 - p1);
vector left = cross(up, v0);
// ハーフベクトル
vector h = v0 + v1*-1;
// 直線に限りなく近い場合はレフトベクトルをハーフベクトルとする
if(acos(dot(v0, v1)) < 0.01)
{
vector new_pos = p1 + offset * normalize(left);
setpointattrib(0, "P", pts[i], new_pos);
}
else
{
// レフトベクトルとハーフベクトルの内積の逆数をオフセット距離に掛ける
float d = dot(left, normalize(h));
vector new_pos = p1 + offset * normalize(h) / d;
setpointattrib(0, "P", pts[i], new_pos);
}
}
}