始点と終点のベクトルを線形補間して中間点に適用する

環境：Houdini 20.5.487

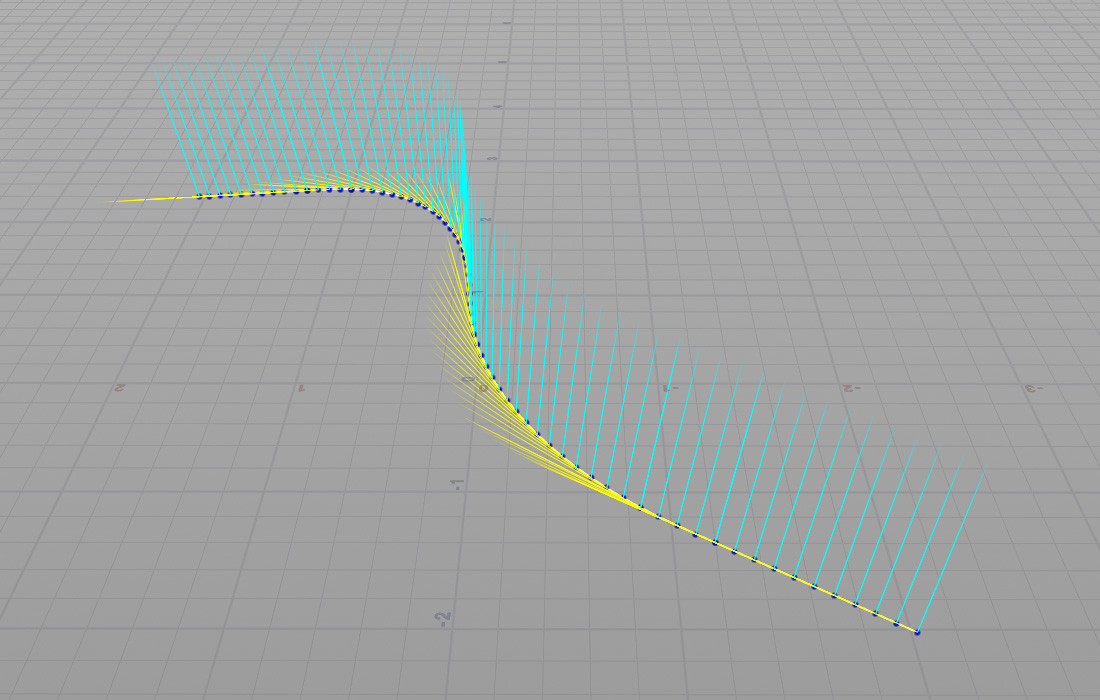
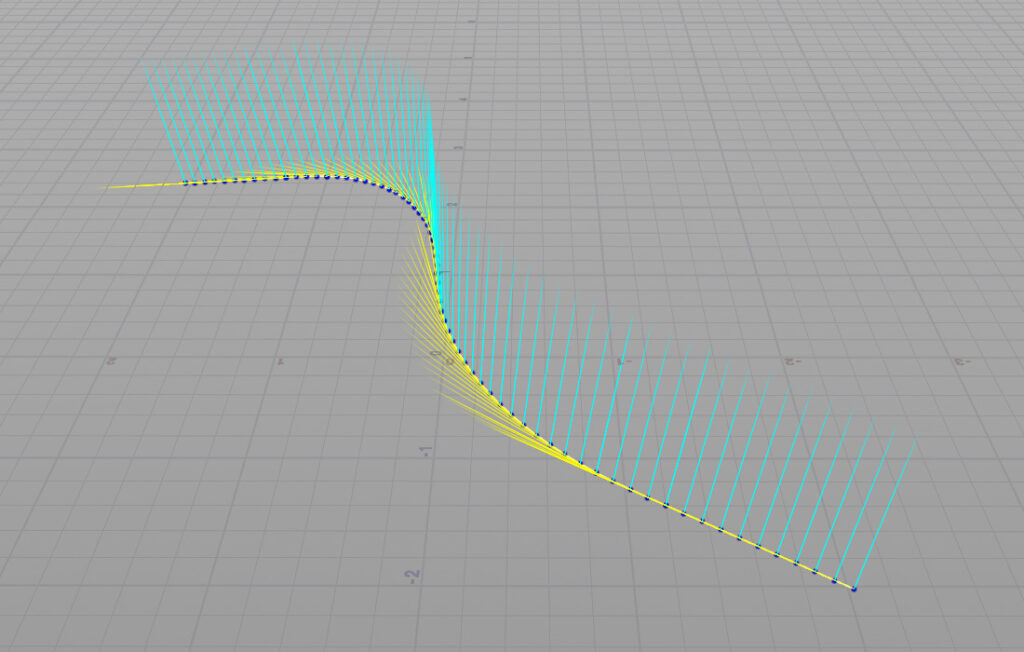
ポリラインの始点と終点に設定されているベクトルNとupを線形補完して中間ポイントに適用していく。

ノードネットワーク
コード

ノードネットワーク

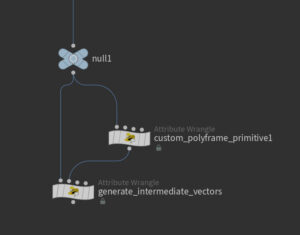
各ポイントの行列を作るためにpolyframeでNとupベクトルを計算する。それを参考にしながら始点と終点を線形補完しながら座標変換して各ベクトルを計算していく。

input1につなぐカスタムPolyframeはこちらを参考に
カスタムPolyframe

コード

//
// 始点と終点のベクトルを線形補間して中間点に適用する
// RunOver: Primitives
//

int pts[] = primpoints(0, @primnum);

// 始点
vector p0 = point(0, "P", pts[0]);
vector n0 = point(0, "N", pts[0]);
vector up0 = point(0, "up", pts[0]);

int index;
vector uv;
xyzdist(1, p0, index, uv);
vector N = primuv(1, "N", index, uv);
vector UP = primuv(1, "up", index, uv);

// 逆行列を掛けてローカル空間のベクトルを取得する
matrix world = maketransform(N, UP);
matrix inverse = invert(world);
n0 *= inverse;
up0 *= inverse;

// 終点
vector p1 = point(0, "P", pts[-1]);
vector n1 = point(0, "N", pts[-1]);
vector up1 = point(0, "up", pts[-1]);

xyzdist(1, p1, index, uv);
N = primuv(1, "N", index, uv);
UP = primuv(1, "up", index, uv);

// 逆行列を掛けてローカル空間のベクトルを取得する
world = maketransform(N, UP);
inverse = invert(world);
n1 *= inverse;
up1 *= inverse;

// 中間点
for(int i = 1; i < len(pts)-1; i++)
{
    vector pos = point(0, "P", pts[i]);
    xyzdist(1, pos, index, uv);
    N = primuv(1, "N", index, uv);
    UP = primuv(1, "up", index, uv);
    
    world = maketransform(N, UP);
    
    vector n2 = lerp(n0, n1, uv.x) * world;
    setpointattrib(0, "N", pts[i], n2);
    
    vector up2 = lerp(up0, up1, uv.x) * world;
    setpointattrib(0, "up", pts[i], up2);
}