環境:Houdini 20.0.751
XZ平面上でポリラインに矩形を並べていきます。

ノードネットワーク
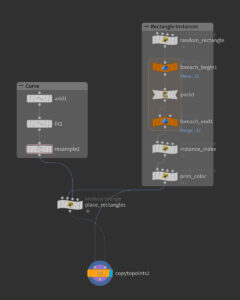
用意するものは、カーブと、Packした矩形インスタンス。
矩形のインスタンス

Z軸方向がカーブの進行方向に沿う方角になる。Z軸の長さをf@width、X軸の長さをf@heightとして、Pack後のポイントアトリビュートに設定しておく。またi@variantというアトリビュートに矩形の種類を入れておき、Copy to Points SOPで突き合わせます。
処理の流れ

矩形の幅を半径とした球でカーブを区切りながら、順番に並べていくということをしています。
球と線分の交点
球とカーブで交差を取ると、基本的には前後で2つ交点が見つかるので、進行方向のみに限定しています。
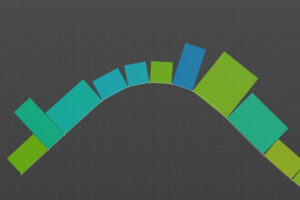
山折りで並んでいる時はそのまま並べても問題ありませんが・・


谷折りで並んだ場合はお互いが干渉するので、オフセットする必要があります。
矩形のオフセットは厳密な計算ではなく、重なっている部分の長さだけ「カーブ上」で進めています。なので急カーブになるほど誤差が発生します。あくまで緩いカーブを想定した仕様としています。
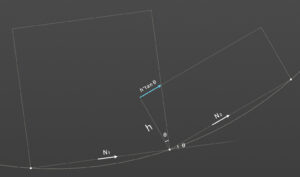
角度θはN1とN2の内積で求め、オフセットする長さはheight*tanθとしている。
コード
ポイントをカーブ上に配置する(place_rectangles)
//
// カーブを円で区切って座標を探していき、矩形を配置していく
// input1: Point Instances
// input2: Curve
// Run Over: Detail
//
// 球とポリラインの交差判定
int spherePolylineIntersection(int geometry; int primnum; vector position; float radius; export vector cross)
{
int result = -1;
int pts[] = primpoints(geometry, primnum);
for(int i = 0; i < len(pts)-1; i++)
{
// 球の中心
vector offset = position;
vector p0 = point(geometry, "P", pts[i]) - offset;
vector p1 = point(geometry, "P", pts[i+1]) - offset;
vector v = normalize(p0 - p1);
float a = v.x * v.x + v.y * v.y + v.z * v.z;
float b = 2 * (p0.x * v.x + p0.y * v.y + p0.z * v.z);
float c = p0.x * p0.x + p0.y * p0.y + p0.z * p0.z - radius * radius;
// 解があるかチェック
if((b * b - 4 * a * c) >= 0)
{
/*
// 判別式±の+の場合
float t = (-b + sqrt(b * b - 4 * a * c)) / 2 * a;
cross = p0 + v * t;
// 直線上にあるかチェック
if(dot(p0 - cross, p1 - cross) < 0)
{
cross += offset;
result = 1;
break;
}
*/
// 判別式±の-の場合
float t = (-b - sqrt(b * b - 4 * a * c)) / 2 * a;
cross = p0 + v * t;
// 直線上にあるかチェック
if(dot(p0 - cross, p1 - cross) < 0)
{
cross += offset;
result = 1;
break;
}
}
}
return result;
}
// カーブの全長
float curveLength = primintrinsic(2, "measuredperimeter", 0);
// 矩形のピボット座標
vector pos = primuv(2, "P", 0, set(0, 0));
vector oldPos = pos; // ひとつ前の矩形の座標
// 各矩形の処理
for(int i = 0; i < npoints(1); i++)
{
float width = prim(1, "width", i);
float height = prim(1, "height", i);
// ひとつ前の矩形と高さを比べ、低いほうを選ぶ
if(i > 0)
{
float prevHeight = prim(1, "height", i-1);
height = min(height, prevHeight);
}
// 矩形の長さを半径とした円とカーブとの交点を探す
vector cross;
if(spherePolylineIntersection(2, 0, pos, width, cross) > 0)
{
int index;
vector start_uv; // 開始位置のパラメトリック座標を記録
xyzdist(2, pos, index, start_uv);
vector oldN = normalize(pos - oldPos);
vector left = cross(set(0,1,0), oldN); // 従法線を外積から求め、これと比較することで谷折り山折りを判定する
// 角度が修正されるので、再計算を繰り返して補正していく
// (posとcrossはループ毎に更新されていく)
for(int j = 0; j < 8; j++)
{
vector N = normalize(cross - pos);
// 谷折りの場合はオフセットする
if(dot(left, N) > 0)
{
N = normalize(cross - pos);
float theta = acos(dot(N, oldN));
float offset = height * sin(theta);
// オフセット値をパラメトリック空間でオフセットする
vector uv = set((start_uv.x * curveLength + offset) / curveLength, 0, 0); // オフセット後のパラメトリック座標
pos = primuv(2, "P", index, uv); // パラメトリック座標からワールド座標を取得
spherePolylineIntersection(2, 0, pos, width, cross); // 交点を更新
}
}
int pt = addpoint(0, pos);
setpointattrib(0, "N", pt, normalize(cross - pos)); // 交点から現在位置へのベクトルへ矩形が傾くようにする
setpointattrib(0, "variant", pt, i); // copy to points SOPで突き合わせる
oldPos = pos; // 前回位置に現在位置を保存
pos = cross; // 現在位置を交点に移動する
}
}

