環境:Houdini 20.0.751
カーブポリラインの高さを、始点と終点のベクトルは維持したままバーチカル曲線(放物線)を使って整える。

元のポリラインカーブはポイントのアトリビュートにフォワードベクトルのNが設定されていることが前提。
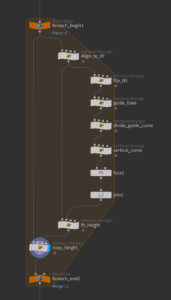
ノードネットワークはこのような感じ。Foreach Primitivesでポリラインごとに処理している。
XY平面にポリラインを投影する(Align_to_XY)
バーチカル曲線が2次元の計算なので平面に投影する。フォワードベクトルのNも行列で座標変換させる。
ポリラインを平面へ投影する

//
// ポリラインをXY平面に投影する
// RunOver: Primitives
//
int pts[] = primpoints(0, @primnum);
float sum = 0;
for(int i = 0; i < len(pts); i++)
{
// position
vector p = point(0, "P", pts[i]);
if(i == 0)
{
setpointattrib(0, "P", pts[i], set(0, p.y, 0));
}
else
{
vector prev = point(0, "P", pts[i-1]);
float length = sqrt(pow(prev.x - p.x, 2) + pow(prev.z - p.z, 2));
sum += length;
setpointattrib(0, "P", pts[i], set(sum, p.y, 0));
}
// N
vector p0 = point(0, "P", pts[i]);
vector p1 = point(0, "P", pts[i+1]);
if(i == len(pts)-1)
{
p0 = point(0, "P", pts[i-1]);
p1 = point(0, "P", pts[i]);
}
// 水平軸のマトリックスをつくる
vector N = normalize(p1 - p0);
vector up = set(0, 1, 0);
vector left = cross(up, N);
N = cross(left, up);
matrix world = maketransform(N, up);
matrix inverse = invert(world);
// 格納されているNの値を取得する
vector N2 = point(0, "N", pts[i]);
N2 *= inverse;
// XY平面へ座標変換する
world = maketransform(set(1,0,0), set(0,1,0));
N2 *= world;
setpointattrib(0, "N", pts[i], N2);
}端のベクトルを内向きに反転する(flip_N)
ガイドのカーブをつくるために両端のフォワードベクトルで外に向いている場合は内向きに反転させる。
//
// 端のベクトルを内向きに向ける
// Run Over: Primitives
//
int pts[] = primpoints(0, @primnum);
vector p0 = point(0, "P", pts[0]);
vector p1 = point(0, "P", pts[1]);
vector N = point(0, "N", pts[0]);
if(dot(N, p1-p0) < 0)
{
N *= -1;
setpointattrib(0, "N", pts[0], N);
}
vector p2 = point(0, "P", pts[-1]);
vector p3 = point(0, "P", pts[-2]);
N = point(0, "N", pts[-1]);
if(dot(N, p3-p2) < 0)
{
N *= -1;
setpointattrib(0, "N", pts[-1], N);
}ガイドカーブを生成する(guide_lines)

両端のフォワードベクトル同士を直線とした場合に、間に交点があれば3点のカーブ、なければ4点のカーブをつくる。
//
// ガイドのラインを生成する
// 向かい合うベクトルの交点が間にない場合は3次ベジェ曲線用の4点ガイドを生成する
// Run Over: Primitives
//
//
// 直線の交点を求める関数(XY平面)
//
vector CrossPointXY(vector p0; vector p1; vector p2; vector p3)
{
// 線分が交差していた場合、直線の交点座標を計算する
float a1 = p0.y - p1.y;
float b1 = p1.x - p0.x;
float c1 = (p1.x - p0.x) * p0.y - (p1.y - p0.y) * p0.x;
float a2 = p2.y - p3.y;
float b2 = p3.x - p2.x;
float c2 = (p3.x - p2.x) * p2.y - (p3.y - p2.y) * p2.x;
float x = (c1 * b2 - c2 * b1) / (a1 * b2 - a2 * b1);
float y = (a1 * c2 - a2 * c1) / (a1 * b2 - a2 * b1);
return set(x, y, 0);
}
int pts[] = primpoints(0, @primnum);
vector p0 = point(0, "P", pts[0]);
vector p1 = point(0, "P", pts[-1]);
vector n0 = point(0, "N", pts[0]);
vector n1 = point(0, "N", pts[-1]);
// Polyline作成
int prim = addprim(0, "polyline");
// 交点座標
vector cross = (p0 + p1) / 2;
if(degrees(acos(dot(n0, -n1))) > 1.0) // 成す角が1度以上だったら
cross = CrossPointXY(p0, p0 + n0, p1, p1 + n1);
// 成す角と閾値(30度以下なら4ポイントカーブにする)
float angle = acos(dot(normalize(n0*-1), normalize(n1)));
float thleshold = radians(30);
// 交点がp0-p1間に存在する
if(dot(cross-p0, p0-p1) < 0 && dot(cross-p1, p1-p0) < 0 && angle > thleshold)
{
// 始点
int pt = addpoint(0, p0);
addvertex(0, prim, pt);
// 交点
pt = addpoint(0, cross);
addvertex(0, prim, pt);
// 終点
pt = addpoint(0, p1);
addvertex(0, prim, pt);
}
else
{
// ベジェ曲線用の4点ガイドカーブを作成する
float L = length(p1-p0);
int pt = addpoint(0, p0);
addvertex(0, prim, pt);
cross = p0 + n0 * L / 4.0;
pt = addpoint(0, cross);
addvertex(0, prim, pt);
cross = p1 + n1 * L / 4.0;
pt = addpoint(0, cross);
addvertex(0, prim, pt);
pt = addpoint(0, p1);
addvertex(0, prim, pt);
}
removeprim(0, @primnum, 1);3点カーブに分割(divide_guide_curve)
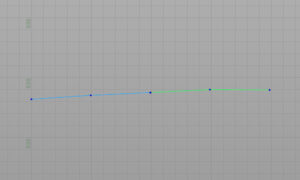
4点カーブなら2つの3点カーブに分割する。
ポリラインをベジェ制御点に分割する
//
// ポリラインをベジェ曲線(2次)のガイドラインへ分割する
// 両隣のエッジの長さの比で分割する
//
// Run Over: Primitives
// input0: Polyline
//
int pts[] = primpoints(0, @primnum);
// 始点と終点が同じインデックスで取得されてしまう場合は最後のインデックスを削除する
if(pts[0] == pts[-1])
removeindex(pts, -1);
//printf('pts:' + sprintf('%g', pts) + '\n');
if(len(pts) > 1)
{
// Polylineが連環しているか否か
int isClosed = primintrinsic(0, "closed", 0);
if(isClosed)
{
// 連環している場合は終点が始点と同じなのでその1つ前はpts[-2]になる
for(int i = 0; i < len(pts); i++)
{
// 3点を選ぶ
vector p0 = point(0, "P", pts[i]);
vector p1 = point(0, "P", pts[i+1]);
vector p2 = point(0, "P", pts[i+2]);
if(i == 0)
{
// p(-1)-p0、p1-p2の比でp0をスライド
// p0-p1とp2-p3の比でp2をスライド
vector prev = point(0, "P", pts[i-1]);
vector p3 = point(0, "P", pts[i+3]);
float t0 = length(p0 - prev) / (length(p0 - prev) + length(p2 - p1));
float t1 = length(p1 - p0) / (length(p1 - p0) + length(p3 - p2));
p0 = p0 * (1-t0) + p1 * t0;
p2 = p1 * (1-t1) + p2 * t1;
}
//
else if(i > 0 && i < len(pts)-1)
{
// p(-1)-p0、p1-p2の比でp0をスライド
// p0-p1とp2-p3の比でp2をスライド
vector prev = point(0, "P", pts[i-1]);
vector p3 = point(0, "P", pts[(i+3)%len(pts)]);
float t0 = length(p0 - prev) / (length(p0 - prev) + length(p2 - p1));
float t1 = length(p1 - p0) / (length(p1 - p0) + length(p3 - p2));
p0 = p0 * (1-t0) + p1 * t0;
p2 = p1 * (1-t1) + p2 * t1;
}
// 終点と終点のひとつ前
else
{
// p(-1)-p0、p1-p2の比でp0をスライド
vector prev = point(0, "P", pts[i-1]);
p1 = point(0, "P", pts[(i+1)%len(pts)]);
p2 = point(0, "P", pts[(i+2)%len(pts)]);
vector p3 = point(0, "P", pts[(i+3)%len(pts)]);
float t0 = length(p0 - prev) / (length(p0 - prev) + length(p2 - p1));
float t1 = length(p1 - p0) / (length(p1 - p0) + length(p3 - p2));
p0 = p0 * (1-t0) + p1 * t0;
p2 = p1 * (1-t1) + p2 * t1;
}
//
// ポリラインを生成
//
{
int prim = addprim(0, "polyline");
int pt = addpoint(0, p0);
addvertex(0, prim, pt);
pt = addpoint(0, p1);
addvertex(0, prim, pt);
pt = addpoint(0, p2);
addvertex(0, prim, pt);
float hue = (i / (float)((len(pts)-2) * 2)) * -1 + 0.6;
setprimattrib(0, "Cd", prim, hsvtorgb(hue, 1, 1));
}
}
}
else
{
for(int i = 0; i < len(pts)-2; i++)
{
// 3点を選ぶ
vector p0 = point(0, "P", pts[i]);
vector p1 = point(0, "P", pts[i+1]);
vector p2 = point(0, "P", pts[i+2]);
// 始点
if(i == 0)
{
// p0-p1とp2-p3の比でp2の位置を移動する
if(len(pts) > 3)
{
vector p3 = point(0, "P", pts[i+3]);
float t = length(p1 - p0) / (length(p1 - p0) + length(p3- p2));
p2 = p1 * (1 - t) + p2 * t;
}
}
//
else if(i > 0 && i < len(pts)-3)
{
// p(-1)-p0、p1-p2の比でp0をスライド
// p0-p1とp2-p3の比でp2をスライド
vector prev = point(0, "P", pts[i-1]);
vector p3 = point(0, "P", pts[i+3]);
float t0 = length(p0 - prev) / (length(p0 - prev) + length(p2 - p1));
float t1 = length(p1 - p0) / (length(p1 - p0) + length(p3 - p2));
p0 = p0 * (1-t0) + p1 * t0;
p2 = p1 * (1-t1) + p2 * t1;
}
// 終点(の2つ前)
else
{
// p(-1)-p0、p1-p2の比でp0をスライド
vector prev = point(0, "P", pts[i-1]);
float t = length(p0 - prev) / (length(p0 - prev) + length(p2 - p1));
p0 = p0 * (1-t) + p1 * t;
}
//
// ポリラインを生成
//
int prim = addprim(0, "polyline");
int pt = addpoint(0, p0);
addvertex(0, prim, pt);
pt = addpoint(0, p1);
addvertex(0, prim, pt);
pt = addpoint(0, p2);
addvertex(0, prim, pt);
// デバッグのためのカラー
float hue = (i / (float)((len(pts)-2) * 2)) * -1 + 0.6;
setprimattrib(0, "Cd", prim, hsvtorgb(hue, 1, 1));
}
}
// 元のポリラインを削除
removeprim(0, @primnum, 1);
}バーチカルカーブを描く(vertical_curve)
3点のガイドカーブをバーチカル曲線に変換する。
バーチカル曲線の描画

//
// ガイドポリラインをバーチカル曲線に変換する
// Run Over: Primitives
//
//
// 直線の交点を求める関数
//
vector CrossPointXY(vector p0; vector p1; vector p2; vector p3)
{
// 線分が交差していた場合、直線の交点座標を計算する
float a1 = p0.y - p1.y;
float b1 = p1.x - p0.x;
float c1 = (p1.x - p0.x) * p0.y - (p1.y - p0.y) * p0.x;
float a2 = p2.y - p3.y;
float b2 = p3.x - p2.x;
float c2 = (p3.x - p2.x) * p2.y - (p3.y - p2.y) * p2.x;
float x = (c1 * b2 - c2 * b1) / (a1 * b2 - a2 * b1);
float y = (a1 * c2 - a2 * c1) / (a1 * b2 - a2 * b1);
return set(x, y, 0);
}
//
// y = (i1-i2) / (2 * L) * x^2
//
// 水平長(バーチカル曲線の最大距離)
float L = 100;
int pts[] = primpoints(0, @primnum);
vector p0 = point(0, "P", pts[0]);
vector p1 = point(0, "P", pts[1]);
vector p2 = point(0, "P", pts[2]);
// 傾き
float i1 = (p1.y - p0.y) / (p1.x - p0.x);
float i2 = (p2.y - p1.y) / (p2.x - p1.x);
// バーチカル曲線の水平長より辺が短かったらバーチカル曲線の長さを短縮する
float length0 = (p1.x-p0.x)*2;
float length1 = (p2.x-p1.x)*2;
L = min(length1, min(length0, L));
// バーチカル曲線の始点の座標を求める
float x = p1.x - L/2;
vector cross = CrossPointXY(p0, p1, set(x, -1000, 0), set(x, 1000, 0));
vector curvePos[]; // バーチカル曲線の座標リスト
int num = 100;
float dist = L / float(num-1);
for(int i = 0; i < num; i++)
{
x = dist * i;
float y = i1 * x - (i1-i2) / (2 * L) * pow(x,2);
curvePos[i] = cross + set(x, y, 0);
}
// ポリライン(始点からの直線)の生成
int prim = addprim(0, "polyline");
int pt = addpoint(0, pts[0]);
addvertex(0, prim, pt);
pt = addpoint(0, curvePos[0]);
addvertex(0, prim, pt);
// ポリライン(バーチカル曲線部分)の生成
prim = addprim(0, "polyline");
// 谷か山かを判別する
vector left = cross(set(0,0,1), p1-p0);
float d = dot(left, p2-p1);
vector slopeColor = set(1, 0.5, 0); // 山
if(d > 0) slopeColor = set(0, 0.5, 1.0); // 谷
for(int i = 0; i < len(curvePos); i++)
{
int pt2 = addpoint(0, curvePos[i]);
addvertex(0, prim, pt2);
setpointattrib(0, "Cd", pt2, slopeColor);
}
// ポリライン(終点までの曲線)の生成
prim = addprim(0, "polyline");
pt = addpoint(0, curvePos[-1]);
addvertex(0, prim, pt);
pt = addpoint(0, pts[2]);
addvertex(0, prim, pt);
// 元のポリラインを削除
removeprim(0, @primnum, 1);このあとFuse Sopでポイントをつなぎ、Join SOPでひとつながりのポリラインにする。
投影した元のカーブの高さをバーチカル曲線に合わせる(fit_height)
縦方向に交差判定をして、高さを交点へ合わせる。
線分の交差判定と交点座標
//
// 線分の交差判定
//
int IsIntersectLinesXY(vector A; vector B; vector C; vector D; export vector Cross)
{
// 直線にタッチしているポイントも考慮するための許容誤差
float epsilon = 0.0001;
int result = -1;
float denominator = (B.y - A.y) * (D.x - C.x) - (B.x - A.x) * (D.y - C.y);
if(denominator != 0)
{
float s = ((B.x - A.x) * (C.y - A.y) - (B.y - A.y) * (C.x - A.x)) / denominator;
if(s >= 0 - epsilon && s <= 1.0 + epsilon)
{
float r = ((A.x - C.x) * (D.y - C.y) - (A.y - C.y) * (D.x - C.x)) / denominator;
if(r >= 0 - epsilon && r <= 1.0 + epsilon)
{
result = 1;
Cross = A + (B - A) * r;
}
}
}
return result;
}
int pts[] = primpoints(1, 0);
for(int i = 0; i < len(pts)-1; i++)
{
vector p0 = point(1, "P", pts[i]);
vector p1 = point(1, "P", pts[i+1]);
vector cross;
int isCross = IsIntersectLinesXY(p0, p1, @P + set(0,-100,0), @P + set(0,100,0), cross);
if(isCross > 0)
{
@P = cross;
break;
}
}ポイントの高さをコピーする(copy_height)

XY平面に投影したカーブの高さだけ元のカーブに戻す。
vector pos = point(1, "P", @ptnum);
@P.y = pos.y;