ポリラインの高さを滑らかにする

環境：Houdini 20.0.751

ターンが１つだけのシンプルなカーブポリラインを3次ベジェ曲線を使って高さだけ整えます。

元のポリラインカーブ。ポイントのアトリビュートにフォワードベクトルのNが設定されていることが前提です。

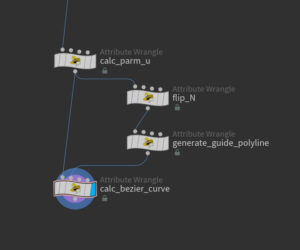
ノードネットワークはこのような感じで、ベジェ曲線生成用のポリラインを分岐してつくります。

パラメトリック座標の計算（calc_parm_u）

ポリラインにおけるポイントごとのパラメトリック座標を計算する。

//
// UVの真っ直ぐ伸ばした場合のパラメトリック座標を計算する
// Run Over: Primitives
//
float curveLength = 0;
float length[];
int pts[] = primpoints(0, @primnum);
for(int i = 1; i < len(pts); i++)
{
    vector p0 = point(0, "P", pts[i-1]);
    vector p1 = point(0, "P", pts[i]);
    length[i] = length(p1-p0);
    // 水平長だけを考慮する場合はこちら
    //length[i] = sqrt(pow((p1-p0).x, 2)+pow((p1-p0).z, 2));
    curveLength += length[i];
}

float pos = 0;
for(int i = 0; i < len(pts); i++)
{
    pos += length[i];
    setpointattrib(0, "__u", pts[i], pos / curveLength);
}

端のベクトルの向きを反転させる（flip_N）

端のポイントのNベクトルが外向きなら内向きに反転する。これはベジェ曲線のガイドカーブをつくるため。

//
// 端のベクトルを内向きに向ける
// Run Over: Primitives
//
int pts[] = primpoints(0, @primnum);

vector p0 = point(0, "P", pts[0]);
vector p1 = point(0, "P", pts[1]);

vector N = point(0, "N", pts[0]);
if(dot(N, p1-p0) < 0)
{
    N *= -1;
    setpointattrib(0, "N", pts[0], N);
}

vector p2 = point(0, "P", pts[-1]);
vector p3 = point(0, "P", pts[-2]);

N = point(0, "N", pts[-1]);
if(dot(N, p3-p2) < 0)
{
    N *= -1;
    setpointattrib(0, "N", pts[-1], N);
}

ガイドのポリラインをつくる（generate_guide_polyline）

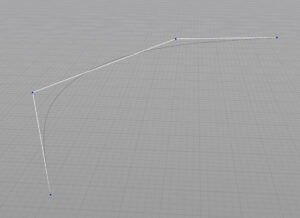
ガイドのポリラインを端のポイントからつくる。お互いの距離の\(\frac{1}{3}\)程度のところに2番目と3番目のポイントを置く。

//
// 4点ガイドのポリラインを作成する
// Run Over: Primitives
//
int pts[] = primpoints(0, @primnum);

vector p0 = point(0, "P", pts[0]);
vector p3 = point(0, "P", pts[-1]);

vector v0 = point(0, "N", pts[0]);
vector v1 = point(0, "N", pts[-1]);

float dist = length(p3 - p0);

vector p1 = p0 + v0 * dist / 3.0;
vector p2 = p3 + v1 * dist / 3.0;

int prim = addprim(0, "polyline");
int pt = addpoint(0, p0);
addvertex(0, prim, pt);

pt = addpoint(0, p1);
addvertex(0, prim, pt);

pt = addpoint(0, p2);
addvertex(0, prim, pt);

pt = addpoint(0, p3);
addvertex(0, prim, pt);

removeprim(0, @primnum, 1);

ベジェ曲線を計算する（calc_bezier_curve）

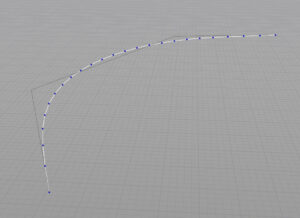
ベジェ曲線をガイドカーブから計算し、Y座標の結果だけ元のポイントに割り当てる。ベジェ曲線にはポイントのパラメトリック座標を使う。

//
// ベジェ曲線を計算し、高さだけ座標にセットする
//
int pts2[] = primpoints(1, @primnum);
vector p0 = point(1, "P", pts2[0]);
vector p1 = point(1, "P", pts2[1]);
vector p2 = point(1, "P", pts2[2]);
vector p3 = point(1, "P", pts2[3]);

int pts[] = primpoints(0, @primnum);
for(int i = 0; i < len(pts); i++)
{
    float t = point(0, "__u", pts[i]);
    
    vector curvePos = (1-t)*(1-t)*(1-t)*p0 + 3*(1-t)*(1-t)*t*p1 + 3*(1-t)*t*t*p2 + t*t*t*p3;

    vector pos = point(0, "P", pts[i]);
    
    pos.y = curvePos.y;
    setpointattrib(0, "P", pts[i], pos);
}

これで縦断勾配が線形補完された勾配のカーブになる。