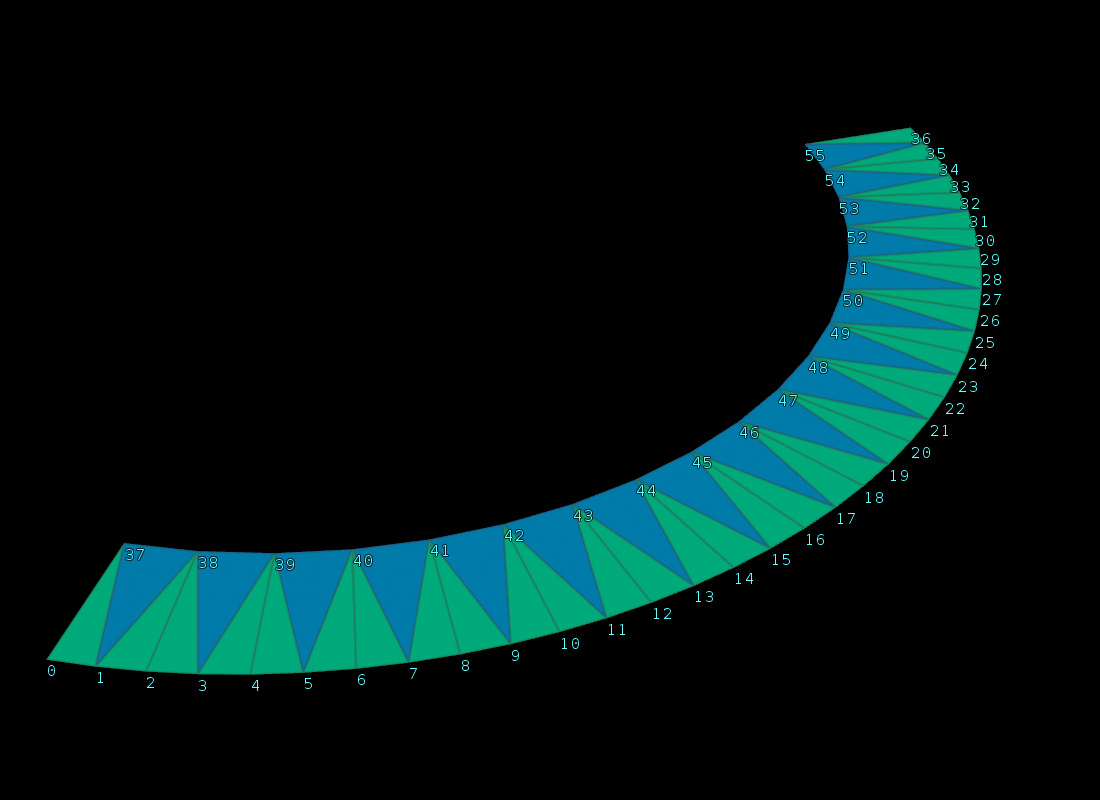
2本のポリラインの間を縫合するようにメッシュを生成します。
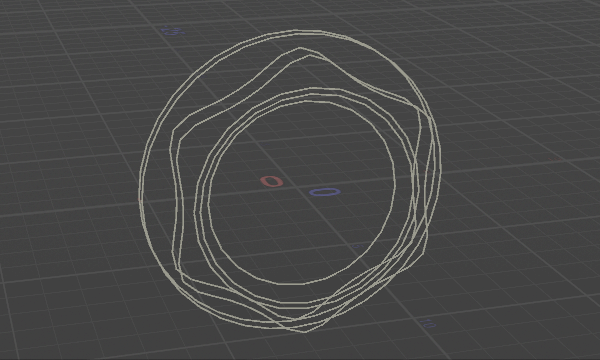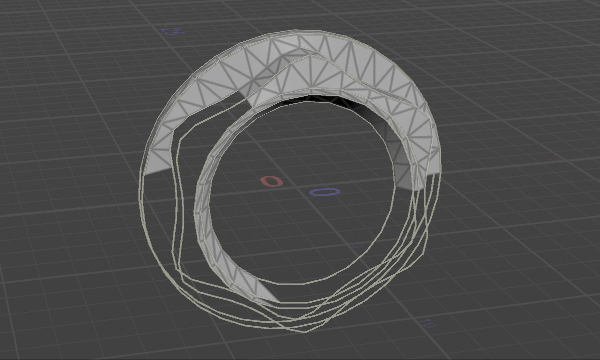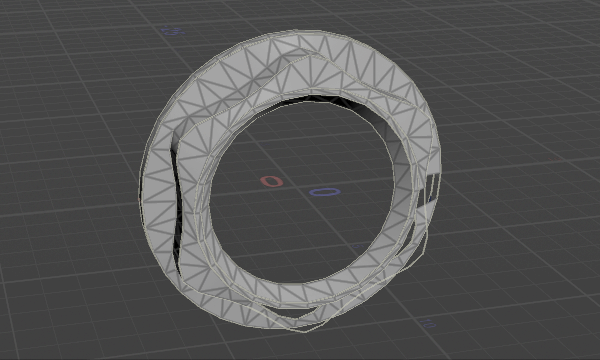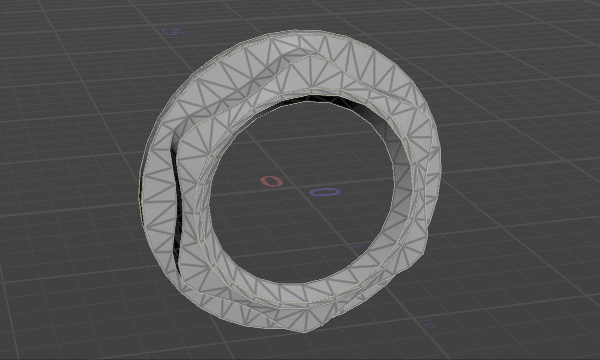
ポリライン同士が同じ方向に並んでおり、交差していないことが前提となります。
処理の流れ
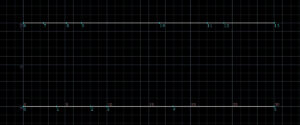
2本のポリラインを用意して、上下のポイントを左から順につないでいきます。下のラインを基準に処理を行っていきます。
基本となる考え方ですが、上下のポイントのX座標を比較して、上のポイントが下のポイントを越えていなかったら下のポイントが頂点で上を底辺とした逆三角形をつくり、越えていたら下を底辺にした三角形をつくり、次のポイントに進みます。これの繰り返しです。
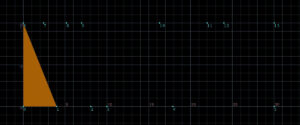
0から5までのポイントをループ処理していきます。0番目のポイントと6番目のポイントを比較し、同じ座標(越えているとみなす)なので、0番目と6番目と、底辺の次のポイントである1番目のポイントで三角形をつくり、次に進みます。
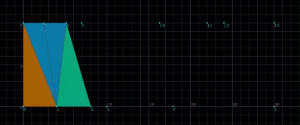
1番目と6番目を見ると、越えていないので逆三角形をつくります。7番目も越えてないので逆三角形をつくります。8番目は越えているので、下を底辺とした三角形をつくり次のポイントへ進みます。また8番目のポイントは次に比較するポイントとして設定しておきます。
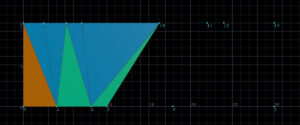
2番目のポイントを基準に、8番目、9番目は越えてないので逆三角形をつくり、10番目は越えているので三角形をつくり、次へ進みます。10番目のポイントは次に比較するポイントとして設定しておきます。
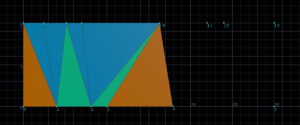
3番目と10番目を比較して下を底辺とした三角形をつくり、次に進みます。

4番目と10番目、11番目を比較して三角形をつくり、次へ進みます。
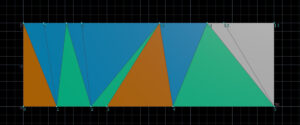
最後のポイントに到達したので、上の残ったポイントで三角形を連続でつくっていき、処理を終わります。(逆に上のラインが最後のポイントに到達したら、そこを頂点にして三角形で埋めていきます)
コードにしてみる
上記の処理の流れをコードにしたものです。
//
// ポリライン間をメッシュで埋める
// Run Over: Detail
//
int pts1[] = primpoints(0, 0); // 列1のポイント
int pts2[] = primpoints(0, 1); // 列2のポイント
// 列2のスタート位置
int count = 0;
for(int i = 0; i < len(pts1); i++)
{
// 列1最後のポイントに到達した場合
if(i == len(pts1)-1)
{
// 列2の残りのポイントを三角形で埋めていく
for(int j = count; j < len(pts2)-1; j++)
{
int prim = addprim(0, "poly");
addvertex(0, prim, pts1[i]);
addvertex(0, prim, pts2[j]);
addvertex(0, prim, pts2[j+1]);
}
}
// 列1の最初から最後手前まで
else
{
// 列2のポイントが最後に到達してしまった場合
if(count == len(pts2)-1)
{
// 列2のポイントはそのままに列1を三角形で埋めていく
int prim = addprim(0, "poly");
addvertex(0, prim, pts1[i]);
addvertex(0, prim, pts2[count]);
addvertex(0, prim, pts1[i+1]);
}
else
{
vector p0 = point(0, "P", pts1[i]);
vector p1 = point(0, "P", pts1[i+1]);
vector t0 = point(0, "P", pts2[count]);
// 列2のポイントが列1のポイントを越えていない
if(t0.x < p0.x)
{
for(int j = count; j < len(pts2); j++)
{
t0 = point(0, "P", pts2[j]);
// 列2のポイント位置が列1のポイントを越えた場合
// 三角形をつくって次のターンへ
if(p0.x < t0.x)
{
int prim = addprim(0, "poly");
addvertex(0, prim, pts1[i]);
addvertex(0, prim, pts2[j]);
addvertex(0, prim, pts1[i+1]);
setprimattrib(0, "Cd", prim, set(0.0,1.0,0.5)); // Green
count = j;
break;
}
else
{
int prim = addprim(0, "poly");
addvertex(0, prim, pts1[i]);
addvertex(0, prim, pts2[j]);
addvertex(0, prim, pts2[j+1]);
setprimattrib(0, "Cd", prim, set(0.0,0.5,1.0)); // Blue
}
}
}
else
{
int prim = addprim(0, "poly");
addvertex(0, prim, pts1[i]);
addvertex(0, prim, pts2[count]);
addvertex(0, prim, pts1[i+1]);
setprimattrib(0, "Cd", prim, set(1.0,0.3,0)); // Orange
}
}
}
//printf('count: ' + sprintf('%g', count) + '\n');
}
removeprim(0, 0, 0);
removeprim(0, 1, 0);実用的なコード
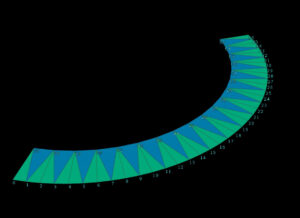
行列を使って軸に縛られない縫合。各ポイントで行列をつくり、ローカル空間のX軸座標を比較することで縫合を進めていきます。
//
// ポリラインをポリゴンで縫合していく
// Run Over: Detail
// input0: Polylines
//
for(int n = 0; n < nprimitives(0)-1; n++)
{
int pts1[] = primpoints(0, n); // 列1のポイント
int pts2[] = primpoints(0, n+1); // 列2のポイント
// スタート位置
int count = 0;
for(int i = 0; i < len(pts1); i++)
{
// 列1最後のポイント
if(i == len(pts1)-1)
{
// 列2の残りのポイントを三角形で埋めていく
for(int j = count; j < len(pts2)-1; j++)
{
int prim = addprim(0, "poly");
addvertex(0, prim, pts1[i]);
addvertex(0, prim, pts2[j]);
addvertex(0, prim, pts2[j+1]);
}
}
// 列1最初から最後手前まで
else
{
// 列2のポイントが最後に到達してしまった場合
if(count == len(pts2)-1)
{
// 列2のポイントはそのままに列1を三角形で埋めていく
int prim = addprim(0, "poly");
addvertex(0, prim, pts1[i]);
addvertex(0, prim, pts2[count]);
addvertex(0, prim, pts1[i+1]);
}
else
{
vector p0 = point(0, "P", pts1[i]);
vector p1 = point(0, "P", pts1[i+1]);
vector t0 = point(0, "P", pts2[count]);
// p0原点の逆行列をつくる
// upベクトルは一番近い隣のポリライン方向にする
vector N = normalize(p1 - p0);
// となりのポリラインの一番近い座標tを求める
int index;
vector uv;
xyzdist(0, itoa(n+1), p0, index, uv);
vector t = primuv(0, "P", index, uv);
vector up = normalize(t-p0);
vector left = normalize(cross(up, N));
up = normalize(cross(N, left));
matrix world = maketransform(N, up, p0);
matrix inverse = invert(world);
p0 *= inverse;
t0 *= inverse;
// 列2のポイントが列1のポイントを越えていない
if(t0.z < p0.z)
{
for(int j = count; j < len(pts2); j++)
{
t0 = point(0, "P", pts2[j]);
t0 *= inverse;
// 列2のポイント位置が列1のポイントを越えた場合
// 三角形をつくって次のターンへ
if(p0.z < t0.z)
{
int prim = addprim(0, "poly");
addvertex(0, prim, pts1[i]);
addvertex(0, prim, pts2[j]);
addvertex(0, prim, pts1[i+1]);
setprimattrib(0, "Cd", prim, set(0.0,1.0,0.5)); // Green
count = j;
break;
}
else
{
int prim = addprim(0, "poly");
addvertex(0, prim, pts1[i]);
addvertex(0, prim, pts2[j]);
addvertex(0, prim, pts2[j+1]);
setprimattrib(0, "Cd", prim, set(0.0,0.5,1.0)); // Blue
}
}
}
else
{
int prim = addprim(0, "poly");
addvertex(0, prim, pts1[i]);
addvertex(0, prim, pts2[count]);
addvertex(0, prim, pts1[i+1]);
setprimattrib(0, "Cd", prim, set(0.0,1.0,0.5)); // Green
}
}
}
}
}
// 既存のポリラインを削除
for(int n = 0; n < nprimitives(0); n++)
removeprim(0, n, 1);