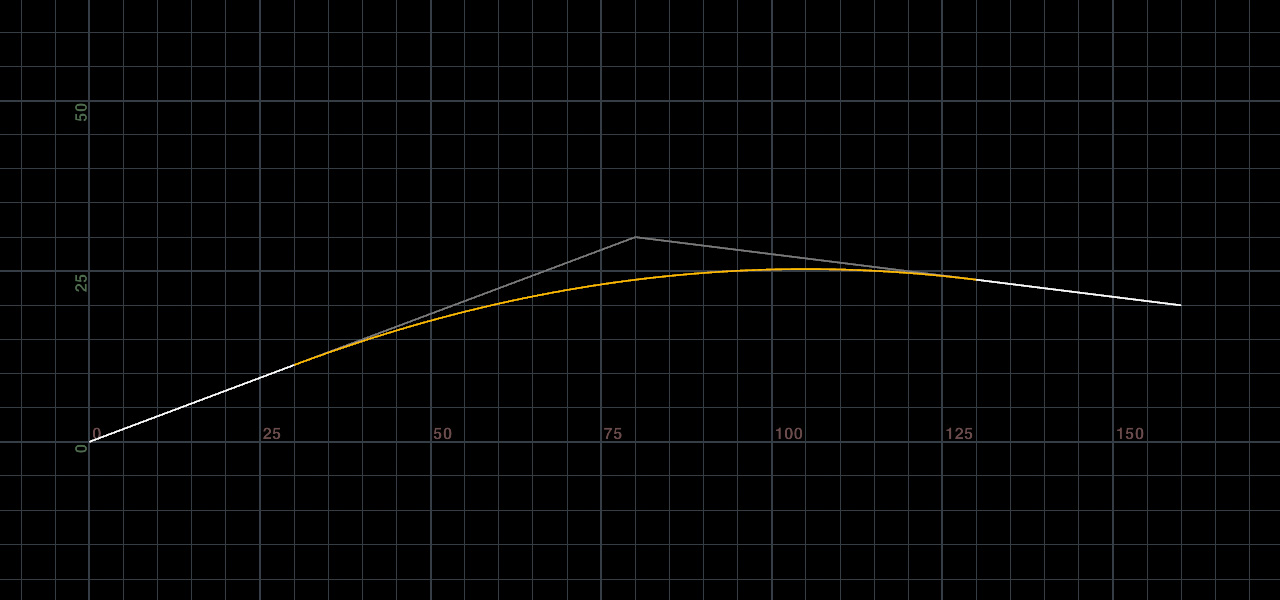
平面上の3つの制御点からバーチカル曲線を描画する。ここではXY平面で計算する。
計算の詳細については以下のページへ
バーチカル曲線
//
// ガイドポリラインをバーチカル曲線に変換する
// Run Over: Primitives
//
// 直線の交点を求める関数
vector CrossPointXY(vector p0; vector p1; vector p2; vector p3)
{
// 線分が交差していた場合、直線の交点座標を計算する
float a1 = p0.y - p1.y;
float b1 = p1.x - p0.x;
float c1 = (p1.x - p0.x) * p0.y - (p1.y - p0.y) * p0.x;
float a2 = p2.y - p3.y;
float b2 = p3.x - p2.x;
float c2 = (p3.x - p2.x) * p2.y - (p3.y - p2.y) * p2.x;
float x = (c1 * b2 - c2 * b1) / (a1 * b2 - a2 * b1);
float y = (a1 * c2 - a2 * c1) / (a1 * b2 - a2 * b1);
return set(x, y, 0);
}
//
// y = (i1-i2) / (2 * L) * x^2
//
// 水平長(バーチカル曲線の最大距離)
float L = 100;
int pts[] = primpoints(0, @primnum);
vector p0 = point(0, "P", pts[0]);
vector p1 = point(0, "P", pts[1]);
vector p2 = point(0, "P", pts[2]);
// 傾き
float i1 = (p1.y - p0.y) / (p1.x - p0.x);
float i2 = (p2.y - p1.y) / (p2.x - p1.x);
// バーチカル曲線の水平長より辺が短かったらバーチカル曲線の長さを短縮する
float length0 = (p1.x-p0.x)*2;
float length1 = (p2.x-p1.x)*2;
L = min(length1, min(length0, L));
// バーチカル曲線の始点の座標を求める
float x = p1.x - L/2;
vector cross = CrossPointXY(p0, p1, set(x, -1000, 0), set(x, 1000, 0));
vector curvePos[]; // バーチカル曲線の座標リスト
int num = 100;
float dist = L / float(num-1);
for(int i = 0; i < num; i++)
{
x = dist * i;
float y = i1 * x - (i1-i2) / (2 * L) * pow(x,2);
curvePos[i] = cross + set(x, y, 0);
}
// ポリライン(始点からの直線)の生成
int prim = addprim(0, "polyline");
int pt = addpoint(0, pts[0]);
addvertex(0, prim, pt);
pt = addpoint(0, curvePos[0]);
addvertex(0, prim, pt);
// ポリライン(バーチカル曲線部分)の生成
prim = addprim(0, "polyline");
// 谷か山かを判別する
vector left = cross(set(0,0,1), p1-p0);
float d = dot(left, p2-p1);
vector slopeColor = set(1, 0.5, 0); // 山
if(d > 0) slopeColor = set(0, 0.5, 1.0); // 谷
for(int i = 0; i < len(curvePos); i++)
{
int pt2 = addpoint(0, curvePos[i]);
addvertex(0, prim, pt2);
setpointattrib(0, "Cd", pt2, slopeColor);
}
// ポリライン(終点までの曲線)の生成
prim = addprim(0, "polyline");
pt = addpoint(0, curvePos[-1]);
addvertex(0, prim, pt);
pt = addpoint(0, pts[2]);
addvertex(0, prim, pt);
// 元のポリラインを削除
removeprim(0, @primnum, 1);直線と放物線で構成されたポリラインが出来上がる。