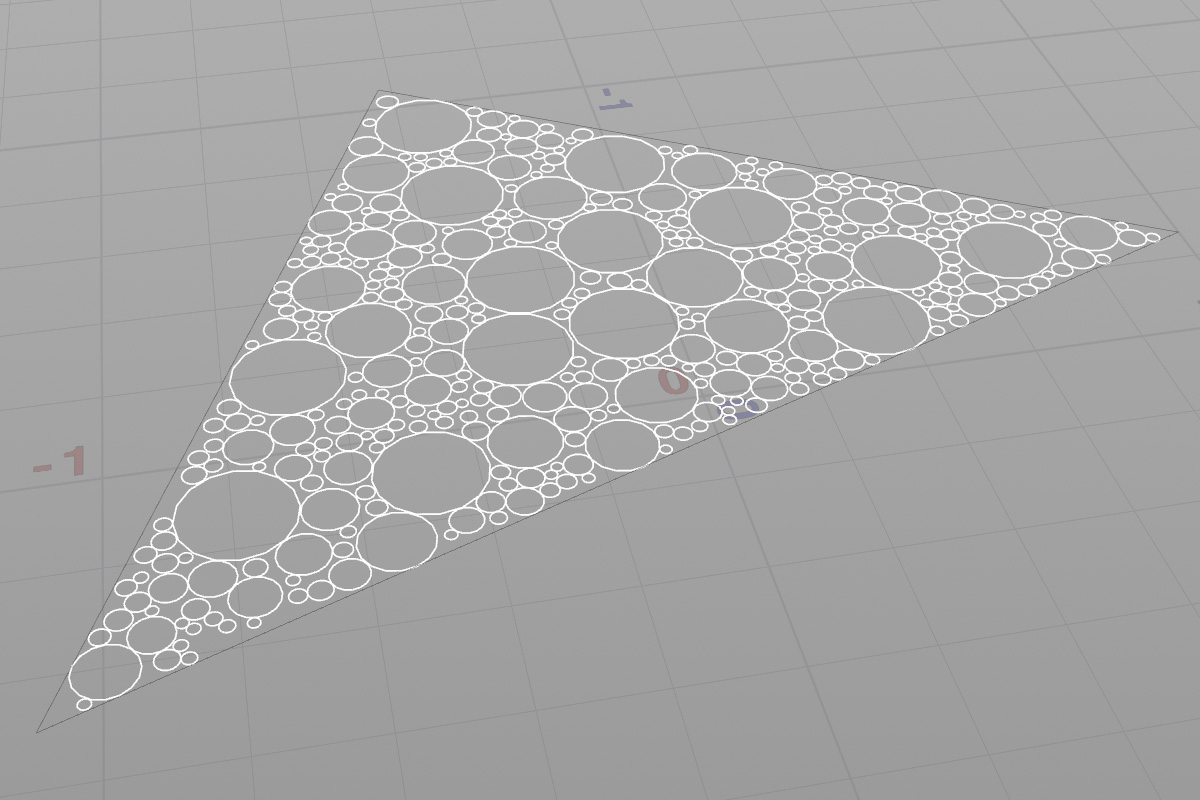
環境:Houdini 20.0.751
円充填に取り組んでみました。

調べているとアルゴリズムは色々ありそうですが、まずは思いついた簡単そうなものからやってみました。隙間が気になるけど今回は多めに見ます。
アルゴリズム
Add SOP等で多角形のポリゴンをつくり、そこにScatter SOPであらかじめ大量のポイントを生成しておく。
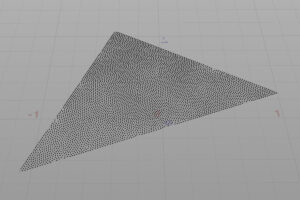
ループ処理を使い、以下を設定した回数だけ繰り返す
1.Scatter SOPで生成したポイントをひとつ取り出す
2.多角形の各エッジとの距離を計算して、エッジに近ければエッジに隣接する半径にする。最小半径よりも近かったら消去。
3.周囲のポイント(円)と比較する。周りにポイントがなければ半径を最大距離にする。距離が近ければ相手の半径に隣接する値にする。遠ければ最大半径にする。相手の半径内だったら消去。
4.生き残ったポイントを生成

大きい円から配置していき、隙間を埋めていくように小さい円を配置していく、という流れです。
ノード構成
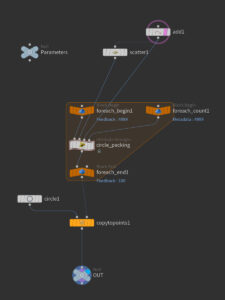
Block BeginのMethodはFetch Feedbackにする。Block EndのIteration MethodはBy Countに。
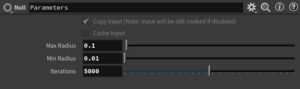
Null SOPにまとめたパラメータ類
・最小半径
・最大半径
・イテレーション回数
Wrangleでポイントを生成し、半径(radius)とスケール(pscale)アトリビュートを設定しておきます。最後にCopy to Points SOPで半径1の円を各ポイントに配置させています。
コード
//
// input0: -
// input1: scattered points
// input2: boundary primitive
// input3: block begin(iteration)
//
// RunOver: Detail
// 円の最大半径と最小半径
float maxRadius = `chs("../Parameters/maxRadius")`;
float minRadius = `chs("../Parameters/minRadius")`;
// イテレーションごとにScatter Pointからポイントを取得する
int iteration = detail(3, "iteration", 0);
vector new_pos = point(1, "P", iteration);
// エッジやポイントとの最短距離
float closeDist = 10000;
// 各ボーダーエッジとの最短距離を計算する
for(int i = 0; i < npoints(2); i++)
{
vector p0 = point(2, "P", i);
vector p1 = point(2, "P", (i+1)%npoints(2));
vector v = normalize(p1 - p0);
float d = dot(new_pos - p0, v);
// 直線の範囲内か判別
float dist = 0;
if(d >= 0 && d <= length(p1-p0))
{
vector p2 = p0 + v * d; // 最短距離の座標
dist = length(p2 - new_pos);
}
// 位置が始点より前の場合
else if(d < 0)
{
dist = length(new_pos - p0);
}
// 位置が終点より後ろの場合
else if(d > length(p1 - p0))
{
dist = length(new_pos - p1);
}
if(dist < closeDist)
closeDist = dist;
}
// ボーダーエッジまでの距離が最小半径より小さかったら終了
if (closeDist < minRadius)
return;
// ボーダーまでの距離を最大半径にクランプしておく
if(closeDist > maxRadius)
closeDist = maxRadius;
// 周りのポイント(円)との距離を比較する
int npts[] = nearpoints(0, new_pos, maxRadius*2);
int closeId = -1;
// まわりにポイントがないならポイントを生成して終了
if(len(npts) == 0)
{
// ポイントを生成する
int pt = addpoint(0, new_pos);
setpointattrib(0, "radius", pt, closeDist);
setpointattrib(0, "pscale", pt, closeDist);
}
else
{
// 他のポイントとの比較
for(int i = 0; i < len(npts); i++)
{
vector n_pos = point(0, "P", npts[i]);
float n_radius = point(0, "radius", npts[i]);
float dist = length(new_pos - n_pos);
float currentRadius = 0;
float rest = dist - n_radius;
// 相手の円の範囲内または円の最小半径以下なら終了
if(dist < n_radius || rest < minRadius)
return;
// 距離の差が最大半径以上なら最大値にクランプする
else if(rest > maxRadius)
currentRadius = maxRadius;
else
currentRadius = rest;
// 他の半径より小さいものを選ぶ
if(currentRadius < closeDist)
closeDist = currentRadius;
}
// ポイントを生成する
int pt = addpoint(0, new_pos);
setpointattrib(0, "radius", pt, closeDist);
setpointattrib(0, "pscale", pt, closeDist);
}各エッジとポイントの距離はこの計算を使っています。
線分と点の距離