リフトの振り子運動

外から加わる力を角速度に変換して、リフトの動きを表現します。

角速度の計算
実装
遠心力

角速度の計算

角速度についてはこのページを参考に
振り子運動と角速度

重力加速度から角速度への変換はこのような図になる。

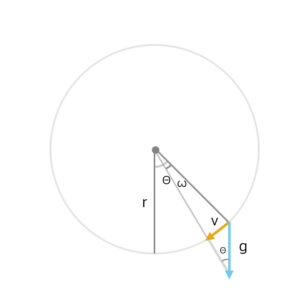
角速度ωの式は、ω = g*sinΘ/r

リフトの進行方向の加速度による影響は以下のような図になる。

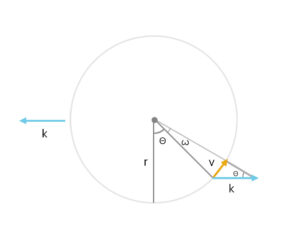
前後の速度差を加速度kとすると、v = k*sinΘになる。v = rωなので、ω = k*sinΘ/rとなり、基本的に重力加速度と考え方は同じ。

実装

カーブに使うポリラインはResampleで均等なポイント配置にして、交互に速度のアトリビュートを12（km/s）、３０（km/s）と設定。その区間を通るたびに速くなったり緩やかになったりするようにしている。

カーブのポイントに持たせているアトリビュート
f@speed：その地点の速度（m/frame）

リフト（ポイント）のアトリビュート
@P, @N, @up：姿勢制御のためのトランスフォーム
f@speed：速度。カーブから毎フレーム取得する。
f@oldSpeed：前フレームの速度。新しい速度との差が加速度になる。
f@dist：ポリラインの始点からの距離
f@radius：振り子の長さ（ｍ）
f@damping：振り子の減衰係数
f@omega_g：重力からの角速度
f@omega_acc：外から受ける加速度からの角速度
f@angle：角度（X軸）

Solver内のWrangle SOP

最初にカーブの情報からポイントの座標や速度の更新をする。

//
// ポリラインから速度を取得して座標を進める
// RunOver: points
// input1: polyline
//

// 加速度（速度の差分）を計算するため、前フレームの速度を記録しておく
f@oldSpeed = f@speed;

// カーブにおける位置に速度を加算する
f@dist += f@speed;

// カーブの長さ
float curveLength = primintrinsic(1, "measuredperimeter", 0);

// UV座標を設定する（0-1のスケール）
float ratio = (f@dist / curveLength) % 1;
vector2 posuv = set(ratio, 0);

// UVからカーブ上の座標を取得し、座標を更新する
vector curvepos = primuv(1, "P", 0, posuv);
@P = curvepos;

// カーブから各値を取得
f@speed =  primuv(1, "speed", 0, posuv); // 速度
@N = primuv(1, "N", 0, posuv);
@up = primuv(1, "up", 0, posuv);

つぎのWrangle SOPでは角速度の計算をする。

進行方向のベクトル（長さは速度）をリフトのローカル空間に変換し、そのZ成分を角速度へ変換している。最後に重力からの角速度も合成して角度に加算している。

//
// 前後の加速度から角速度を計算する
// RunOver: points
//
float gravity = 9.81 / (60 * 60) *-1; // 重力加速度（単位：m/s^2）

// 重力による振り子運動
float acceleration = gravity / f@radius * sin(f@angle); // 角加速度
f@omega_g += acceleration;  // 角速度
f@omega_g -= f@damping * f@omega_g;

// カーブの進行方向を向いた水平な行列をつくる
vector forward = normalize(set(@N.x, 0, @N.z));
matrix world = maketransform(forward, set(0,1,0));
matrix inverse = invert(world);

// 進行ベクトルをローカルに変換
vector localN = (@N * (f@speed - f@oldSpeed)) * inverse;

// 相対的にかかる加速度による振り子運動
float k = localN.z * -1;
float acceleration2 = k * cos(f@angle) / f@radius; // 角加速度
f@omega_acc += acceleration2;  // 角速度
f@omega_acc -= f@damping * f@omega_acc;

// 角度を更新する
f@angle += f@omega_g + f@omega_acc;

最後に角度を@Nと@upに変換する。このポイントにCopy to Points SOPでリフトのメッシュを配置する。

//
// 姿勢（トランスフォーム）のためのベクトルNとupを計算する
// RunOver: points
//

// カーブの軸に沿った、水平な行列をつくる
vector forward = set(@N.x, 0, @N.z);
forward = normalize(forward);
matrix world = maketransform(forward, set(0,1,0));

float z = cos(f@angle);
float y = sin(f@angle);
@N = normalize(set(0, y, z));
vector left = set(-1, 0, 0);
@up = cross(left, @N);

@N *= world;
@up *= world;