パースペクティブ射影変換行列はレンダリングやカリング等に使われている。カメラ視点の平面で内外判定することができるので、対象のオブジェクトがカメラに写っているかを判定するのに便利。
この座標変換をHoudini上で再現してみる。
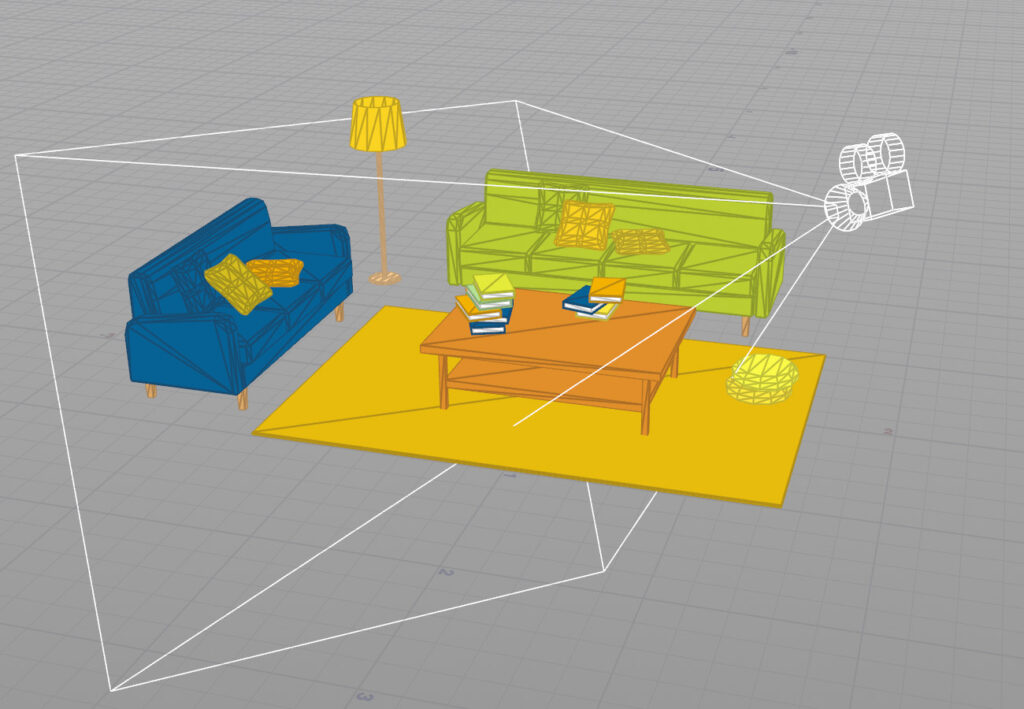

Houdiniで設定したカメラからの視点。焦点距離は67.1769mmで、Apertureは36mmにした。(これは視野角30°に合わせた設定)
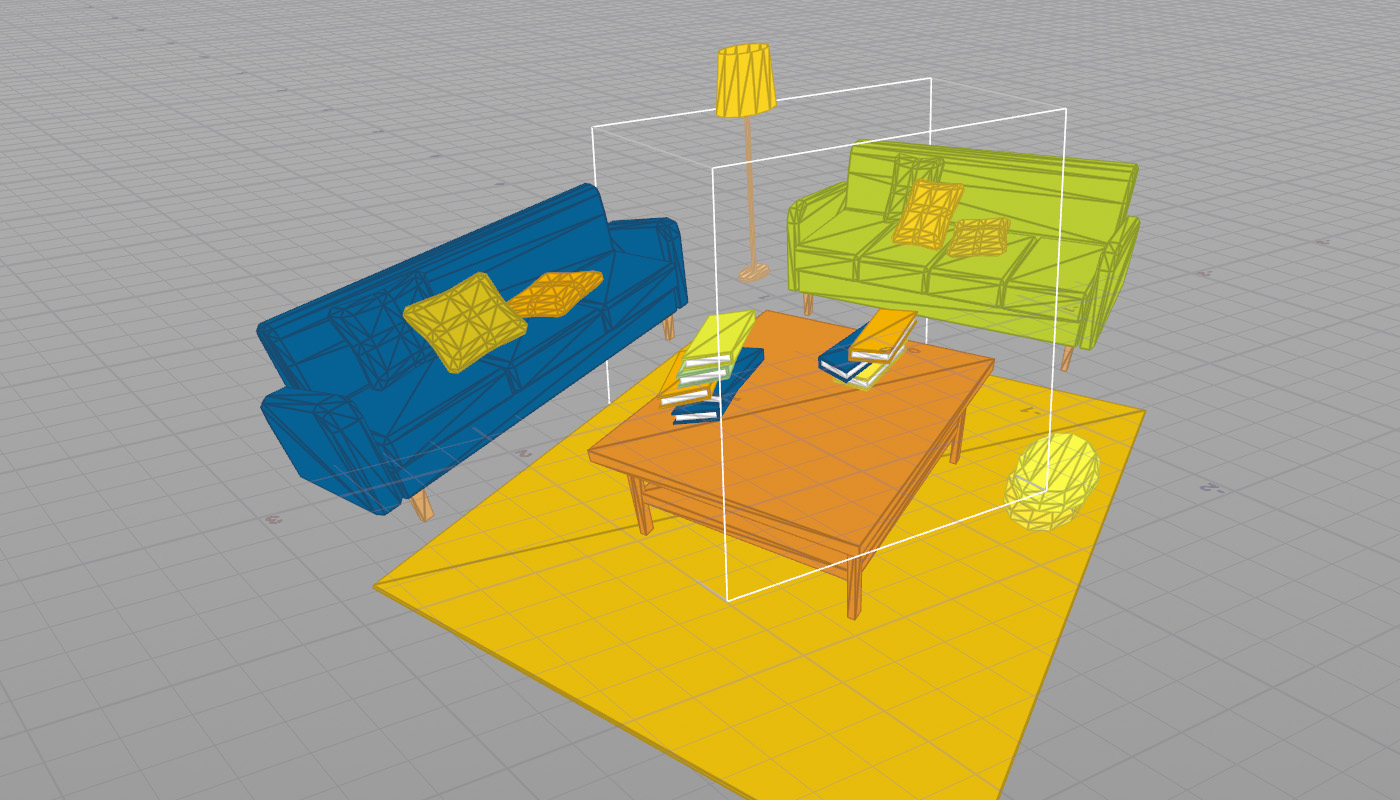
結論から書くと、パースペクティブ射影変換行列はシーン全体を視錐台(Frustum)に収めるということをしている。視錐台は縦横の長さが2で、奥行きが1の立方体に変形する。
画角は30°、Nearクリップは0.1、Farクリップは10、縦と横の長さを1にしている。
ビュー行列
最初にカメラ空間(ビュー行列)に座標を変換する。
//
// カメラの逆行列を掛ける
// RunOver: Points
//
// カメラの行列をつくる
vector N = point(1, "N", 0);
vector up = point(1, "up", 0);
vector P = point(1, "P", 0);
matrix viewWorld = maketransform(N, up, P);
matrix inverseView = invert(viewWorld);
@P *= inverseView;
f@z = @P.z; // カメラ空間のZ座標を記録しておくカメラ空間の座標になる。ここから3つ行列を掛けていく。
アスペクト比の行列
最初はアスペクト比の行列。X軸のスケールを掛けている。

アスペクト比1(そのまま)
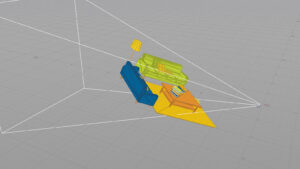
アスペクト比1.6(X軸方向に縮小している)
//
// アスペクト比
// RunOver: Points
//
matrix world = ident();
// 画面の縦横幅
float height = `chs("../controller/height")`;
float width = `chs("../controller/width")`;
float aspectRatio = width / height;
// 正方形に収めるためにアスペクト比の逆数を掛ける
world.xx = 1/ aspectRatio; // 垂直が固定で、水平方向で画面を変化させている
//aspectWorld.yy = aspectRatio; // 水平を固定し、垂直方向で画面を変化させる場合はこちら
// |h/w, 0, 0, 0|
// | 0, 1, 0, 0|
// | 0, 0, 1, 0|
// | 0, 0, 0, 1|
@P *= world;画面の横幅を増やすとメッシュは横に縮小していく。これは最終的に視錐台のX値-1~1の範囲に収めるため。
画角の行列
つづけて遠近感をつける行列を掛けて、XとYの座標を動かす。

変換前
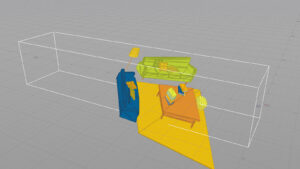
変換後
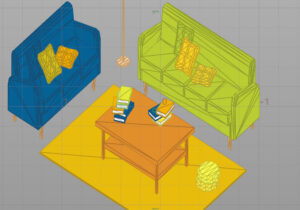
XY平面のオルソ画面にすると、パースがついてない状態。

これに画角と奥行きをつける行列を掛けてパースのついた座標に変換します。
//
// 画角と奥行
//
matrix world = ident();
float theta = radians(60);
world.xx = 1 / (tan(theta/2) * f@z);
world.yy = 1 / (tan(theta/2) * f@z);
// |1/(tan(theta/2)*z), 0, 0, 0|
// |0, 1/(tan(theta/2)*z), 0, 0|
// |0, 0, 1, 0|
// |0, 0, 0, 1|
@P *= world;// 参考に上の行列の値
// |1.19048, 0, 0, 0|
// |0, 1.19048, 0, 0|
// |0, 0, 1, 0|
// |0, 0, 0, 1|絵を描く時の遠近法と同じ要領で、カメラに遠い距離の頂点ほど座標を動かしてパースをつけている。
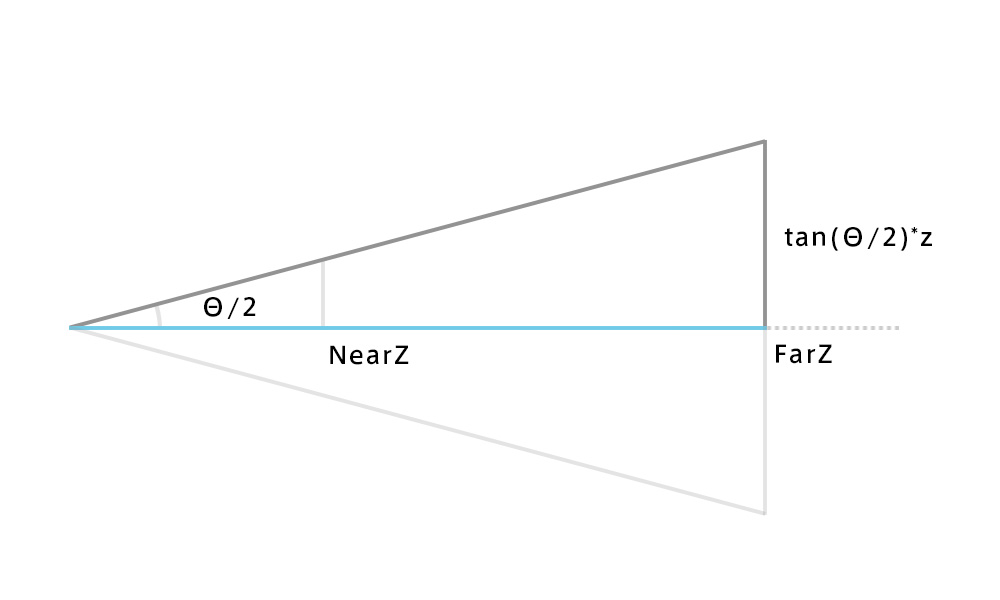
Z軸におけるプレーンの高さはtan(theta/2)*zなので、1/(tan(theta/2)*z)だけXとY方向にスケール変換している。
圧縮をかける行列
最後に、Z軸方向に圧縮する行列を掛ける。

変換前

変換後
//
// -nearZずらして、(farZ-nearZ)をZ方向に圧縮する
//
float nearZ = 0.1;
float farZ = 10;
matrix world = ident();
world.zz = 1.0 / (farZ - nearZ); // 0-1に圧縮
world.wz = -nearZ / (farZ - nearZ); // Z方向のオフセット
// |1, 0, 0, 0|
// |0, 1, 0, 0|
// |0, 0, 1.0/(farZ-nearZ), 0|
// |0, 0, -nearZ/(farZ-nearZ), 1|
@P *= world;Z方向にNearプレーンとFarプレーンの距離を1にするスケールを掛け、Nearプレーンの分だけオフセットして原点に戻している。
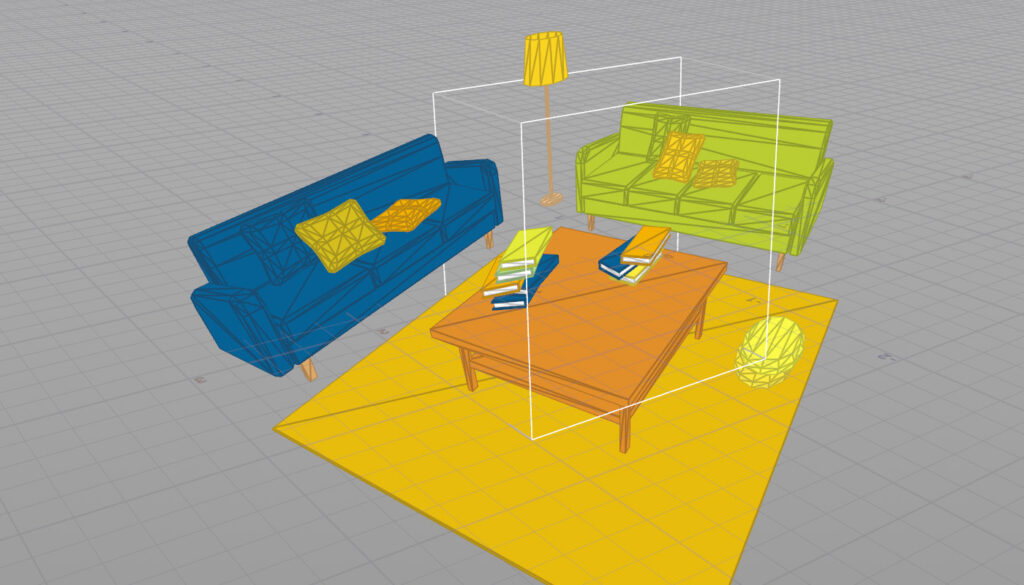
結果。視錐台も直方体に変形している。
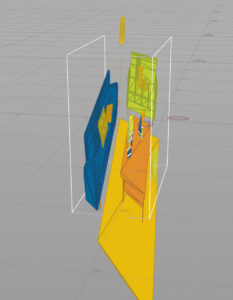
横から見ると0~1の範囲で圧縮されている。ちなみにデプス値(深度値)はこのZの値のこと。手前が0で奥が1。
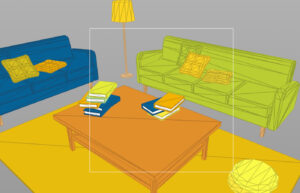
XY平面のオルソ方向から見た画面。

カメラ視点と同じ絵になっている。
視錐台
最後に、デバッグ用に視錐台の各座標の計算。これも画角と距離から三角関数で計算できる。


//
// 視錐台メッシュを作成
//
// 画角、Nearプレーン、Farプレーン、縦横幅
float angle = `chs("../controller/angle")`;
float nearZ = `chs("../controller/nearZ")`;
float farZ = `chs("../controller/farZ")`;
float height = `chs("../controller/height")`;
float width = `chs("../controller/width")`;
float theta = radians(angle);
float aspectRatio = width / height;
float nearFrustumHeight = 2.0 * nearZ * tan(theta * 0.5); // Nearプレーンの高さ
float nearFrustumWidth = nearFrustumHeight * aspectRatio;
float farFrustumHeight = 2.0 * farZ * tan(theta * 0.5); // Farプレーンの高さ
float farFrustumWidth = farFrustumHeight * aspectRatio;
// Nearプレーンの座標
vector p0 = set(nearFrustumWidth * -0.5, nearFrustumHeight * 0.5, nearZ);
vector p1 = set(nearFrustumWidth * 0.5, nearFrustumHeight * 0.5, nearZ);
vector p2 = set(nearFrustumWidth * 0.5, nearFrustumHeight * -0.5, nearZ);
vector p3 = set(nearFrustumWidth * -0.5, nearFrustumHeight * -0.5, nearZ);
// Farプレーンの座標
vector p4 = set(farFrustumWidth * -0.5, farFrustumHeight * 0.5, farZ);
vector p5 = set(farFrustumWidth * 0.5, farFrustumHeight * 0.5, farZ);
vector p6 = set(farFrustumWidth * 0.5, farFrustumHeight * -0.5, farZ);
vector p7 = set(farFrustumWidth * -0.5, farFrustumHeight * -0.5, farZ);
// ポリラインを作成していく
int pt0 = addpoint(0, p0);
int pt1 = addpoint(0, p1);
int pt2 = addpoint(0, p2);
int pt3 = addpoint(0, p3);
int pt4 = addpoint(0, p4);
int pt5 = addpoint(0, p5);
int pt6 = addpoint(0, p6);
int pt7 = addpoint(0, p7);
// Near Clipping Plane
int prim = addprim(0, "polyline");
addvertex(0, prim, pt0);
addvertex(0, prim, pt1);
addvertex(0, prim, pt2);
addvertex(0, prim, pt3);
addvertex(0, prim, pt0);
// Far Clipping Plane
prim = addprim(0, "polyline");
addvertex(0, prim, pt4);
addvertex(0, prim, pt5);
addvertex(0, prim, pt6);
addvertex(0, prim, pt7);
addvertex(0, prim, pt4);
prim = addprim(0, "polyline");
addvertex(0, prim, pt0);
addvertex(0, prim, pt4);
setprimattrib(0, "Cd", prim, set(0.6,0.6,0.6));
prim = addprim(0, "polyline");
addvertex(0, prim, pt1);
addvertex(0, prim, pt5);
setprimattrib(0, "Cd", prim, set(0.6,0.6,0.6));
prim = addprim(0, "polyline");
addvertex(0, prim, pt2);
addvertex(0, prim, pt6);
setprimattrib(0, "Cd", prim, set(0.6,0.6,0.6));
prim = addprim(0, "polyline");
addvertex(0, prim, pt3);
addvertex(0, prim, pt7);
setprimattrib(0, "Cd", prim, set(0.6,0.6,0.6));NearプレーンとFarプレーンの高さを画角から三角関数で計算している。