直線同士の距離を求める

2本の直線を最短で結ぶ直線の交点を求めて距離を計算する。

計算

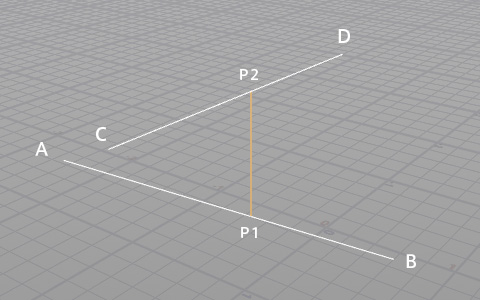
直線ABとCDを最短で結ぶ直線（ベクトル）はどちらの直線とも90度で交差する関係で存在している。つまり、どちらの直線とも内積が０で交わる、と考えて方程式を立てて解いていく。

正規化したベクトルABをab
正規化したベクトルCDをcd
AからP₁までの距離をd₁
CからP₂までの距離をd₂
とすると

P1 = A + d₁ * ab
P2 = C + d₂ * cd

ベクトルP₁P₂は

P₂ – P₁ = C + d₂ * cd – (A + d₁ * ab) = C – A + d₂ * cd – d₁ * ab

ベクトルACをac(※正規化はしてない)としてまとめると

P₁P₂ = ac + d₂ * cd – d₁ * ab

ベクトルAB、ベクトルCDとの内積の式を立てると

ab・(ac + d₂ * cd – d₁ * ab) = 0
cd・(ac + d₂ * cd – d₁ * ab) = 0

式を展開すると

ab・ac + d₂(ab・cd) – d₁(ab・ab) = 0

abは正規化ベクトルなのでab・abは１になる

d₁ = ab・ac + d₂(ab・cd)

同じように

cd・(ac + d₂ * cd – d₁ * ab) = 0

cd・ac + d₂(cd・cd) – d₁(cd・ab) = 0

d₂ = d₁(ab・cd) – cd・ac

この２つの式をそれぞれ代入してまとめる

d₁ = ab・ac + (d₁(ab・cd) – cd・ac)(ab・cd)

d₁ = (ab・ac) + d₁(cd・ab)(ab・cd) – (cd・ac)(ab・cd)

d₁ – d₁(ab・cd)(ab・cd) = (ab・ac) – (cd・ac)(ab・cd)

d₁( 1 – (ab・cd)(ab・cd) ) = (ab・ac) – (cd・ac)(ab・cd)

d₁ = ( (ab・ac) – (cd・ac)(ab・cd) ) / ( 1 – (ab・cd)(ab・cd) )

同じようにd₂をまとめると

d₂ = ( ab・ac + d₂(ab・cd) )(cd・ab) – cd・ac

d₂ = (ab・ac)(ab・cd) + d₂(ab・cd)(ab・cd) – (cd・ac)

d₂ – d₂(ab・cd)(ab・cd) = (ab・ac)(ab・cd) – (cd・ac)

d₂ ( 1 – (ab・cd)(ab・cd) ) = (ab・ac)(ab・cd) – (cd・ac)

d₂ = ( (ab・ac)(ab・cd) – (cd・ac) ) / ( 1 – (ab・cd)(ab・cd) )

となる

コード

// RunOver: Detail

vector a = point(1, "P", 0);
vector b = point(1, "P", 1);
vector ab = normalize(b - a);

vector c = point(2, "P", 0);
vector d = point(2, "P", 1);
vector cd = normalize(d - c);

vector ac = c - a;　// ベクトルACは正規化しない

float d1 = (dot(ab, ac) - dot(ac, cd) * dot(ab, cd)) / (1 - dot(ab, cd) * dot(ab, cd));

vector p1 = a + ab * d1;
int pt1 = addpoint(0, p1);

float d2 = (dot(ab, ac) * dot(ab, cd) - dot(cd, ac)) / (1 - dot(ab, cd) * dot(ab, cd));

vector p2 = c + cd * d2;
int pt2 = addpoint(0, p2);

// ポリラインを生成
int prim = addprim(0, "polyline");
addvertex(0, prim, pt1);
addvertex(0, prim, pt2);

setpointattrib(0, "Cd", pt1, set(1,0.5,0));
setpointattrib(0, "Cd", pt2, set(1,0.5,0));

//printf('d1:' + sprintf('%g', d1) + '\n');