線分と点の距離

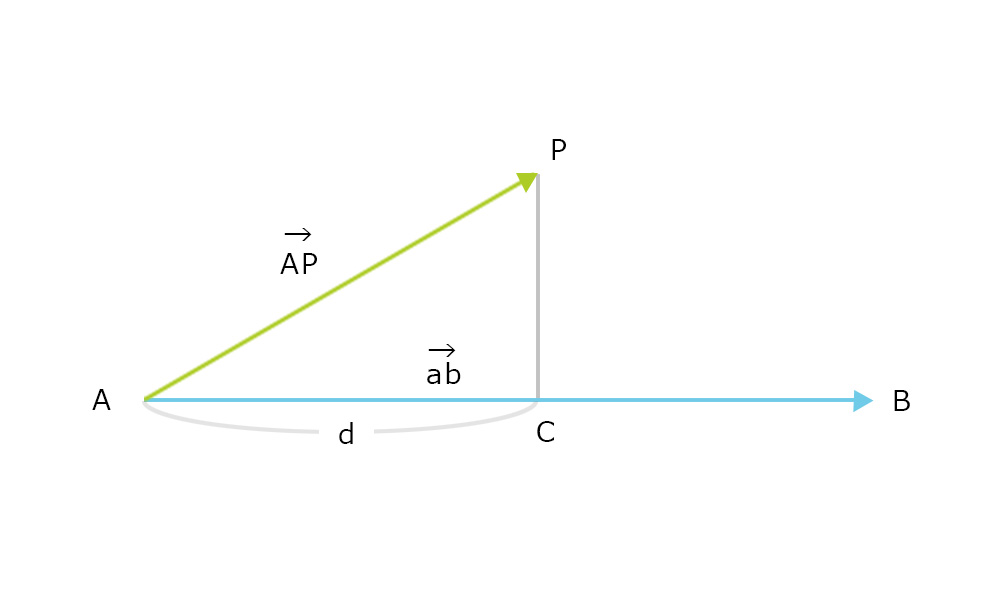
線分ABと点Pの最短距離と交点を求めるには内積を使う。

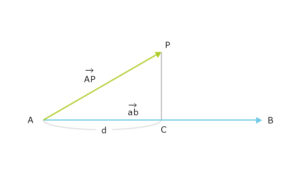
片方のベクトルが正規化されていた場合、内積の値が投影した長さになることを利用する。Aと点Pを結んだベクトルAPと、ベクトルABを正規化したベクトルabの内積はdになる。これによってA+ab*dで交点Cが計算できる。交点Cが分かればPとCの距離（点と直線の最短距離）を求めることができる。

vector ab = normalize(B - A);
float d = dot(P-A, ab);

// 交点座標
vector C = A + ab * d;

実例：ライン
実例：カーブ

実例：ライン

// input0: line
// input1: point
// RunOver: Detail

vector start = point(0, "P", 0);
vector end = point(0, "P", 1);

vector point = point(1, "P", 0);

vector line_vec = normalize(end - start);
vector point_vec = point - start;
float d = (dot(point_vec, line_vec));

// 直線の範囲内か判別
if(d >= 0 && d < length(start - end))
{
    // 交点座標
    vector projection = start + line_vec * d;
    addpoint(0, projection);
}

実例：カーブ

ループで各エッジと比較する。交点座標がエッジ内に収まっているかチェックする。

// input1: point
// input2: polyline

float minDist = 10000;
vector closestCross;

vector point = point(1, "P", 0);

// 各エッジとの交点を比較する
for(int i = 0; i < npoints(2)-1; i++)
{
    vector start = point(2, "P", i);
    vector end = point(2, "P", i+1);
    
    vector line_vec = normalize(end-start);
    float d = dot(point-start, line_vec);
    
    // 直線の範囲内か判別
    if(d >= 0 && d <= length(start-end))
    {
        vector projection = start + line_vec * d;  // 新しいポイント
        
        float dist = length(projection-point);
        
        // 最小の値なら更新
        if(dist < minDist)
        {
            minDist = dist;
            closestCross = projection;
        }
    }
    // 位置が始点より前の場合
    else if(d < 0)
    {
        float dist = length(point-start);
        
        // 最小の値なら更新
        if(dist < minDist)
        {
            minDist = dist;
            closestCross = start;
        }
    }
    // 位置が終点より後ろの場合
    else if(d > length(start-end))
    {
        float dist = length(point-end);
        
        // 最小の値なら更新
        if(dist < minDist)
        {
            minDist = dist;
            closestCross = end;
        }
    }
}

int pt = addpoint(0, closestCross);