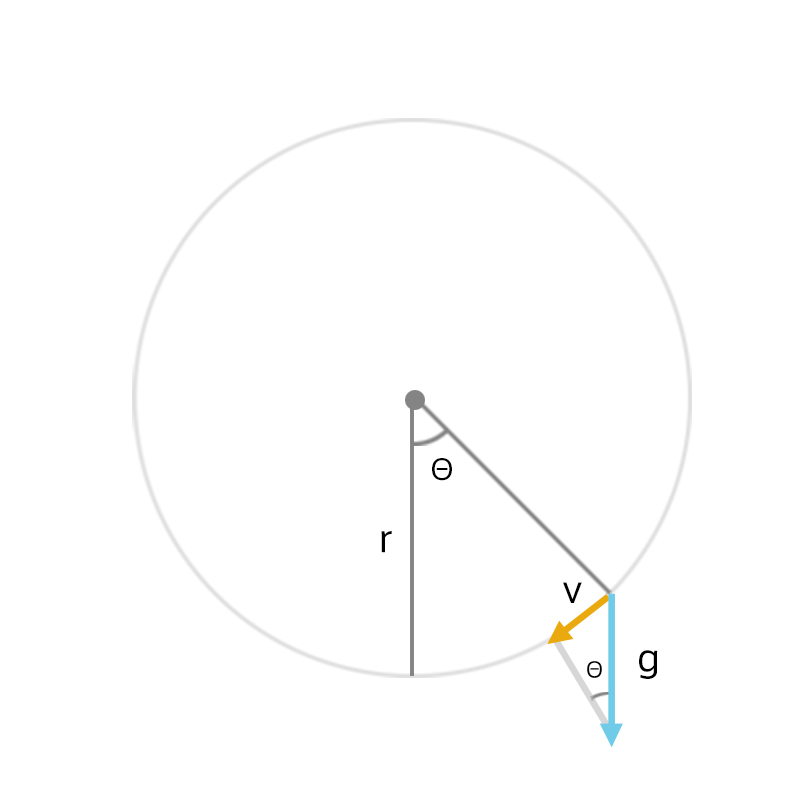
角速度を使う振り子運動について。外から加わる力を回転角に変換する。
角速度
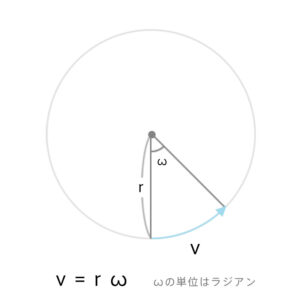
角速度v = rωとなる。ω(オメガ)は角度(ラジアン)。半径Rが1の時、角度=円弧の長さになる。
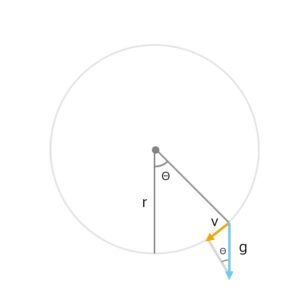
重力から角速度を計算すると、v = g*sinΘになる。
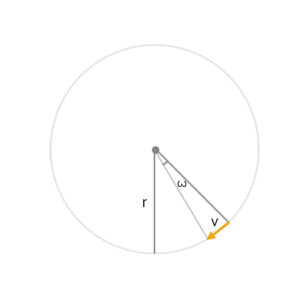
v = rωなので、rω = g*sinΘ
ω = g*sinΘ / rとなる。半径が大きいほど、角速度ωの角度は小さくなる。
外から加わる力を円運動の角度に変換しているところがポイント。
振り子運動
角速度を使って振り子運動を再現してみる。
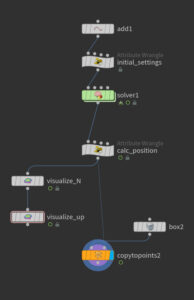
ノードグラフはこのようにした。Add SOPでポイントを1つ追加し、次のWrangleノードで初期設定をしている。
// RunOver: Point
// 振り子の初期角度(単位:rad)
// 0は真下 PIは真上 PI/2は真横
f@angle = PI / 4;
// 角速度ω(rad)
f@omega = 0.0;
// 振動の減衰係数
f@damping = 0.1 / 60.0;
// 振り子の長さ(単位:m)
f@radius = 2.0;dampingが減衰係数で、これが0だと永久に振り子運動することになる。
つぎにSolver SOPの中にWrangleノードをひとつ作成する。これは毎フレーム更新される。
// 振り子運動
// RunOver: Point
// 重力加速度(単位:m/s^2)
float gravity = 9.81 / (60*60) *-1;
// 位置と速度の更新 ω = g*sinΘ / r
float acceleration = gravity * sin(f@angle) / f@radius;
f@omega += acceleration;
f@omega -= f@damping * f@omega;
f@angle += f@omega;60フレームでアニメーションさせているので、重力加速度を時間の平方(60*60)で割っている。
最後に角度をベクトルに変換し、Copy to Points SOPでモデルを配置した。
//
// 角度をベクトルに変換
// RunOver: Points
//
float x = cos(f@angle);
float y = sin(f@angle);
@N = set(0, y, x);
vector left = set(-1, 0, 0);
@up = cross(left, @N);