Polypath SOPとは
ポリラインのトポロジーをクリーンアップし、重複したり分離しているカーブを一本に整理する便利なSOPです。
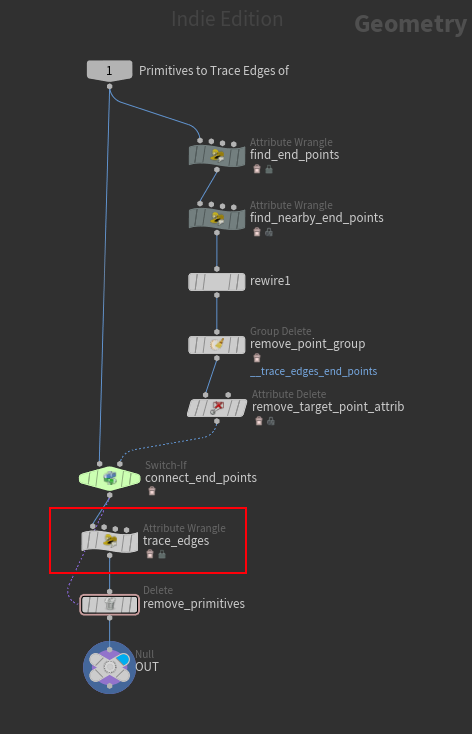
Polypath SOPの中身。trace_edgesが肝の部分で、ここで新しくポリラインを生成している。直後にDelete SOPで元のポリラインを削除する流れ。
trace_edgesの大まかな流れ
すべてのポイントから、交差点または端まで辿っていく
↓
探索している途中で開始ポイントよりも小さい番号に遭遇したらそこで処理を中断する
↓
開始ポイントより小さい番号のポイントに遭遇しないまま端まで到達したら、新しくポリラインを生成する
この条件により重複しないポリラインが生成される。
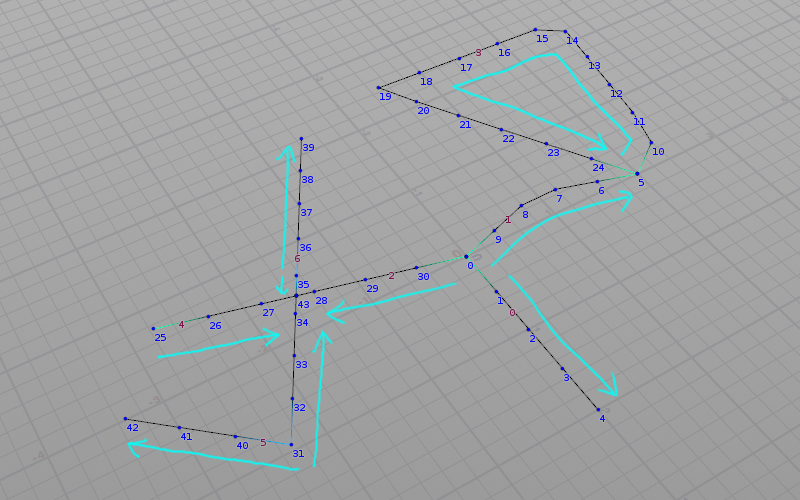
0, 5, 6, 25, 31, 35のポイントは到達点(端、交差点)までに、自分の番号より低いものに遭遇していない
コードの流れ
所々にコメントを追記しています。
void sortedRemoveDuplicates(int a[]) {
int n = len(a);
if (n <= 1) {
return;
}
int prev = a[0];
int desti = 1;
for (int i = 1; i < n; ++i) {
if (a[i] != prev) {
if (i != desti) {
a[desti] = a[i];
}
++desti;
prev = a[i];
}
}
resize(a, desti);
}
int traceEdges(const int ifirst; const int inext; int path[]) {
int prev = ifirst;
int next = inext;
while (1) { // 無限ループ
int adj[] = neighbours(0,next);
adj = sort(adj);
sortedRemoveDuplicates(adj); // 重複の解消
// Ignore any self-loops or back edges
removevalue(adj, next); // 配列から値を削除する
removevalue(adj, prev);
int n = len(adj);
if (n != 1) { // 隣接ポイント数が0、または複数の場合は端のポイントなので終わらせる
// end point: successful path!
break;
}
int other = adj[0];
// If other is a lower point number, it
// "owns" this path.
if (other < ifirst) { // 開始ポイントより番号が小さい場合は終了させる
return 0;
}
// Add other to the path
append(path, other);
prev = next;
next = other;
// If loops back to original, stop and indicate it.
if (other == ifirst) { // 探索ポイントが最初の番号だった場合、ループしているとみなす
return 2;
}
}
return 1; // Breakで抜けた場合は成功フラグ
}
int adj[] = neighbours(0,@ptnum);
adj = sort(adj); // 昇順に並べ替え。例{0, 3, 7, 12}
sortedRemoveDuplicates(adj);
// Ignore any self-loops
removevalue(adj, @ptnum);
int n = len(adj);
if (n == 0) { // 隣接ポイントがないなら終了
return;
}
// Only the lowest-numbered points are designated
// to trace out the paths.
if (n == 1 && @ptnum > adj[0]) { // 隣接ポイントがひとつで、開始ポイントより小さければ終了
return;
}
if (n == 2 && @ptnum > min(adj[0],adj[1])) { // 隣接ポイントの小さい方の値が開始ポイントより小さければ終了
return;
}
// If larger than largest neighbour, can't be min
// on any path.
if (@ptnum > adj[n-1]) { // 一番大きい隣接ポイントより開始ポイントが大きければ終了
return;
}
// Need to trace 2 paths if degree is exactly 2
if (n == 2) {
int path0[] = array(adj[0]);
int path1[];
int success = traceEdges(@ptnum, adj[0], path0);
if (success == 0) {
return;
}
// 2 indicates a loop, so only one path
int loop = (success == 2);
if (!loop) { // ループしてない場合
path1 = array(adj[1]);
success = traceEdges(@ptnum, adj[1], path1);
if (success == 0) {
return;
}
}
int closed = chi("../closeloops") && loop;
int prim = addprim(geoself(), closed ? "poly" : "polyline");
int n0 = len(path0)-closed;
int n1 = len(path1);
for (int i = n1-1; i >= 0; --i) {
addvertex(geoself(), prim, path1[i]);
}
addvertex(geoself(), prim, @ptnum);
for (int i = 0; i < n0; ++i) {
addvertex(geoself(), prim, path0[i]);
}
}
else {
for (int j = 0; j < n; ++j) {
// Only the lowest-numbered points are designated
// to trace out the paths.
if (adj[j] < @ptnum) { // 隣接ポイント番号が始点より小さかったら
continue; // 処理を終了して次のループへ
}
int path[] = array(adj[j]);
int success = traceEdges(@ptnum, adj[j], path);
if (success == 0) { // ポイントをトレースして始点より小さい値が出た場合
continue; // 処理を終了して次のループへ
}
int npath = len(path);
// 2 indicates a loop, so another neighbour must
// be removed
if (success == 2) { // ループしていたらForループから候補を削除する
int other = path[npath-2];
removevalue(adj, other);
--n;
}
int prim = addprim(geoself(), "polyline"); // ループしているポリラインを生成
addvertex(geoself(), prim, @ptnum);
for (int i = 0; i < npath; ++i) {
addvertex(geoself(), prim, path[i]);
}
}
}配列の重複を解消する関数:sortedRemoveDuplicates()
1~18行目。Pythonでいうset()関数のようなもの
昇順に並んだ配列の重複を解消する関数。入力する配列aを{1,1,2,2,2,3,3,4}とすると1から2に切り替わるまでiを進める。もし前回と値が変わった場合、インデックスdestiの場所に値を入れ{1,”2″,2,2,2,3,3,4}、destiの値をひとつ進め、また配列aの新しい値が見つかるまで待機する。最終的に数字が重ならないように詰めていく形で配列が生成される。
エッジを辿っていく関数:traceEdges()
20~57行目。
隣接するポイントを辿っていき、端または交差点へ行き着くまでポイントのリストをつくる。途中始点より小さな番号に当たったら条件不成立ということで終了する。
引数
ifirst: 開始ポイント
inext: 隣接ポイント
path[]: 出力されるポイント配列
返り値
0: 失敗フラグ(捜査したポイントに開始ポイントより小さい値のものがある)
1: 成功フラグ
2: ループフラグ
メイン処理
59行目から。数々の条件をチェックしていき、最後まで残ったポイントからポリラインを生成する。
69行目
隣接ポイントがなければ終了
75行目
隣接ポイントが1つで、開始ポイント(@ptnum)より小さい番号なら終了。
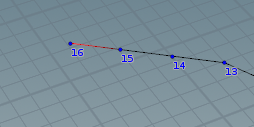
該当例。一番端のポイントのとなりが小さい番号なら終了。16から始まり隣が15なので終了。
78行目
隣接ポイントが2つで、開始ポイント(@ptnum)より両方の番号が小さければ終了
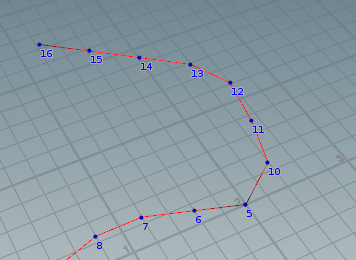
該当例。途中に位置するほとんどのポイントはこれに当たる。10から始まった場合は隣が11と5なので終了。5から始まった場合は隣が10と6なので継続する。
84行目
開始ポイント(@ptnum)が隣接ポイントのいちばん大きい番号より大きかったら終了。ここを起点にラインが生成される可能性はない。
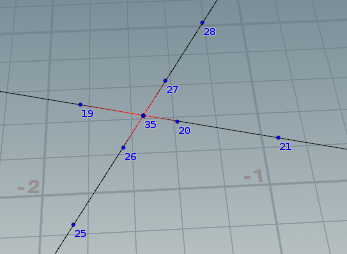
該当例。隣接ポイントで一番大きい27は開始ポイントの35より小さいので終了。
89行目、隣接ポイント数が2つの場合
始点はエッジ上のどこかのポイントということになる。(端や交差点ではない)
隣接するポイントを順に辿っていき、交差点や端に行き着くまで始点より小さな番号が出てこないか探していく。
片方の番号からtraceEdges()を使いエッジ(path0)をトレースする。最後まで始点より大きい数字が続き、パスがつながれば始点から反対側のエッジを捜査して続ける。

上手くいかなかった場合。開始ポイント20から始まり、adj[0]=21から到達した先が0番(始点の20より小さい)なので終了。
ループしていなかったらもう片方の番号からエッジ(path1)をトレースする。同じように最後まで始点より大きい数字が続けば、パスをつなげる。
ポリラインを生成して、path1, path0の順でひとつのラインにつなげていく。
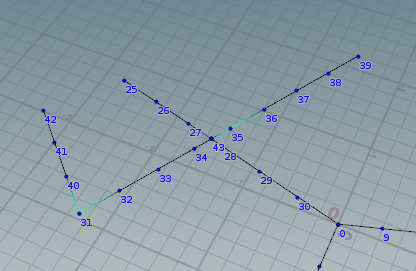
開始ポイント31から、まずadj[0]=32を調べ、{32, 33, 34, 43}と31以上の番号が続くので成立。今度は片方adj[1]=40を調べる。{40, 41, 42}と31以上が続くので成立。{42, 41, 40, 31, 32, 33, 34, 43}とつなげたポリラインを生成する。
118行目、隣接ポイント数が複数の場合
始点は交差点ということになる。
隣接ポイントを順にForループで探索していく。もし辿って行ったポイントが始点より小さければ終了して次のForループへ。もしラインがループしていたらループの最後の番号path[-2]を重複を避けるために隣接ポイントから除外する。
以上の条件をクリアしたら、トレースしたパスの順でつないでポリラインを生成する。
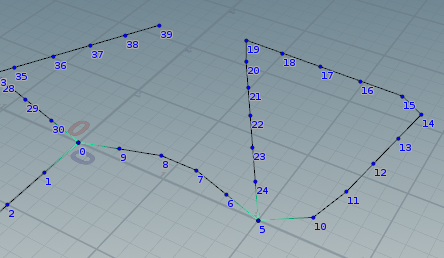
開始ポイント5の隣接ポイントは10, 24, 6。10から探索を始めた場合、path = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 5}とループして終わる。path[-2]は24が該当するので、隣接ポイントから24を除外する。