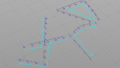
ハーフベクトルを計算することで、進行方向に対してカーブが左右のどちら向きに膨らんでいるか(外向きか内向きか)を判定できる。
前後のポイント座標で計算する
//
// ハーフベクトルを計算する(外側のベクトル)
// Run Over: Primitives
//
float angleThreshold = 0.1; // 閾値(°)、この角度以下は直線と判定する
int pts[] = primpoints(0, @primnum);
for(int i = 1; i < len(pts)-1; i++)
{
int next = (i + 1) % len(pts);
int prev = i - 1;
// p0----->p1<-----p2
vector p0 = point(0, "P", pts[prev]);
vector p1 = point(0, "P", pts[i]);
vector p2 = point(0, "P", pts[next]);
vector v0 = normalize(p1 - p0);
vector v1 = normalize(p1 - p2);
if(acos(dot(v0, v1*-1)) < radians(angleThreshold))
{
setpointattrib(0, "__h", pts[i], set(0,0,0));
}
else
{
vector h = v0 + v1;
setpointattrib(0, "__h", pts[i], h);
}
}パラメトリックUVで計算する
前後のポイント座標ではなく、任意の距離のポリライン上の座標で計算する。この場合、入力するポリラインはResampleされている必要がある。
//
// ポリラインのハーフベクトルを計算する
// (ポリラインはResampleされていることが望ましい)
//
// Run Over: Primitives
//
float step = 5.0; // 計測する幅
float angleThreshold = 0.1; // 閾値(°)、この角度以下は直線と判定する
float curveLength = primintrinsic(0, "measuredperimeter", @primnum);
int pts[] = primpoints(0, @primnum);
for(int i = 1; i < len(pts)-1; i++)
{
vector pos = point(0, "P", pts[i]);
int index;
vector uv;
xyzdist(0, pos, index, uv);
// 端はクランプする
float prevU = clamp(uv.x - (step / curveLength), 0, 1);
float nextU = clamp(uv.x + (step / curveLength), 0, 1);
vector p0 = primuv(0, "P", index, set(prevU, 0));
vector p1 = point(0, "P", pts[i]);
vector p2 = primuv(0, "P", index, set(nextU, 0));
// p0----->p1<-----p2
vector v0 = normalize(p1 - p0);
vector v1 = normalize(p1 - p2);
// 角度の確認
//setpointattrib(0, "angle", pts[i], degrees(acos(dot(v0, v1*-1))));
if(acos(dot(v0, v1*-1)) < radians(angleThreshold))
{
setpointattrib(0, "__h", pts[i], set(0,0,0));
}
else
{
vector h = (v0 + v1);
setpointattrib(0, "__h", pts[i], h);
}
}例

進行方向のレフトベクトルとハーフベクトルの内積を取ることで、カーブのふくらみが右側か左側かを判別できる。
// レフトベクトルとハーフベクトルの内積で進行方向に対して右か左かを判別する
vector left = cross(@up, @N);
float d = dot(left, v@__h);
if(d > 0) @Cd = set(0,1,0.5);
else if(d < 0) @Cd = set(1,1,0);