点と多角形の内外判定（Winding-Numberアルゴリズム）

概要
コード

概要

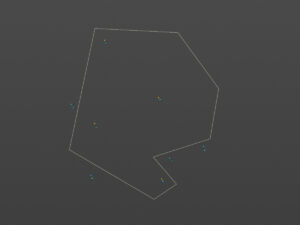
点が多角形に含まれているか否かはWinding Numberアルゴリズムを使って判定できる。多角形の各頂点を周回して得られる角度の合計が、もし内側にある場合は360度になり、外側の場合は0度になる。

コード

調べるポイントごとの処理。input1には多角形のポリラインを入力する。

//
// Winding Number Algorithm
// Run Over: Points
// 

float result = 0;

int pts[] = primpoints(1, 0);
for(int i = 0; i < len(pts); i++)
{
    vector p0 = point(1, "P", pts[i-1]);
    vector p1 = point(1, "P", pts[i]);
    
    vector l0 = p0 - @P;
    vector l1 = p1 - @P;
    
    float angle = acos(dot(normalize(l1), normalize(l0)));
    
    // 進行方向が逆転しているか外積でチェックする
    vector cross = cross(l0, l1);
    if(dot(cross, set(0,1,0)) < 0)
        angle *= -1;
    
    result += angle;
}

if(abs(result) >= 0.01)
    @Cd = set(1,0.5,0);
else
    @Cd = set(0,0.5,1);

ポリラインにねじれがあると進行方向が逆転して正負が変わる。