線分の交差判定と交点座標

関数

XZ平面における交差判定の関数。引数は線分１の始点、終点、線分2の始点、終点、交差座標となる。

//
// 線分の交差判定
//
int IsIntersectLinesXZ(vector A; vector B; vector C; vector D; export vector Cross)
{
    // 直線にタッチしているポイントも考慮するための許容誤差
    float epsilon = 0.0001;
    
    int result = -1;    

    float denominator = (B.z - A.z) * (D.x - C.x) - (B.x - A.x) * (D.z - C.z);
    
    if(denominator != 0)
    {
        float s = ((B.x - A.x) * (C.z - A.z) - (B.z - A.z) * (C.x - A.x)) / denominator;
        if(s >= 0 - epsilon && s <= 1.0 + epsilon)
        {
            float r = ((A.x - C.x) * (D.z - C.z) - (A.z - C.z) * (D.x - C.x)) / denominator;
            
            if(r >= 0 - epsilon && r <= 1.0 + epsilon)
            {
                result = 1;
                Cross = A + (B - A) * r;
            }
        }
    }
    
    return result;
}

変数epsilonに閾値を入れる。小さい値にするほど判定が厳しくなり、大きい値にするほど許容範囲が広くなる。

使用例

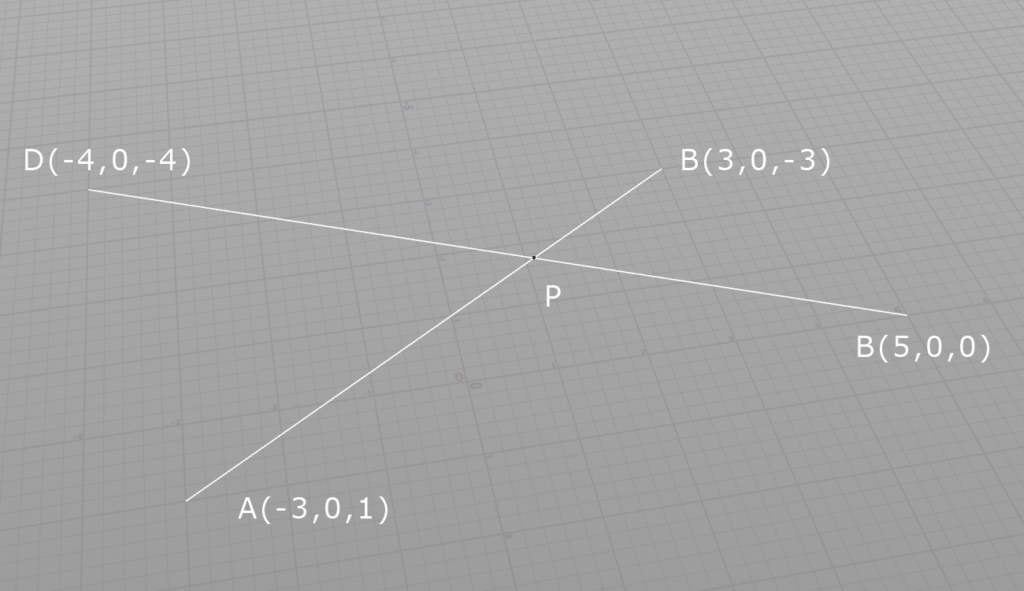
交差座標を格納するベクトル型変数crossを事前に用意している。関数を実行するとcrossに座標が入る。

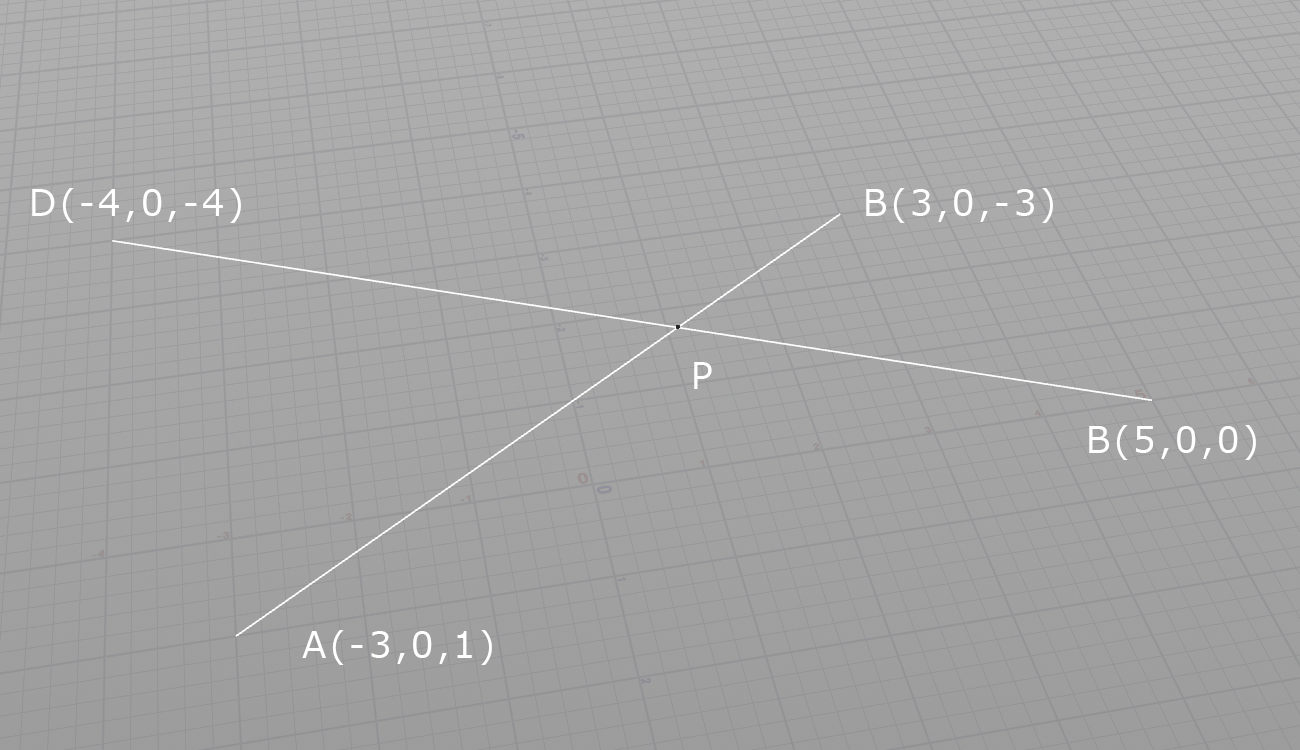
vector A = set(-3,0,1);
vector B = set(3,0,-3);
vector C = set(5,0,0);
vector D = set(-4,0,-4);

vector cross;
int isIntersect = IsIntersectLines(A, B, C, D, cross);

printf(sprintf('%g', isIntersect) + '\n');
// 1
printf(sprintf('%g', cross) + '\n');
// {1.1,0,-1.73333}

解説

線分ABと線分CDを考える。

点Pは線分AB上のポイント、点Qは線分CD上のポイント。

P = A + (B – A) * r
Q = C + (D – C) * s

P=QなのでA + (B – A) * r = C + (D – C) * s

A.x + (B.x – A.x) * r = C.x + (D.x – C.x) * s
A.y + (B.y – A.y) * r = C.y + (D.y – C.y) * s

が成り立つので、

r = ( (C.x – A.x) + (D.x – C.x) * s ) / (B.x – A.x)・・・①

s = ( (A.y – C.y) + (B.y – A.y) * r ) / (D.y – C.y)・・・②

①を変形させる

s = ( (A.x – C.x) + (B.x – A.x) * r ) / (D.x – C.x)

②との等式にすると

( (A.y – C.y) + (B.y – A.y) * r ) / (D.y – C.y) = ( (A.x – C.x) + (B.x – A.x) * r ) / (D.x – C.x)

rでまとめると

r = ( (A.x – C.x) * (D.y – C.y) – (A.y – C.y) * (D.x – C.x) ) / ( (B.y – A.y) * (D.x – C.x) – (B.x – A.x) * (D.y – C.y) )

となる。今度は②を変形させる

r = ( (C.y – A.y) + (D.y – C.y) * s ) / (B.y – A.y)

①との等式にしてまとめると

s = ( (B.x – A.x) * (C.y – A.y) – (B.y – A.y) * (C.x – A.x) ) / ( (B.y – A.y) * (D.x – C.x) – (B.x – A.x) * (D.y – C.y) )

となる。

分母d = ( (B.y – A.y) * (D.x – C.x) – (B.x – A.x) * (D.y – C.y) )

とすると

s = ( (B.x – A.x) * (C.y – A.y) – (B.y – A.y) * (C.x – A.x) ) / d

r = ( (A.x – C.x) * (D.y – C.y) – (A.y – C.y) * (D.x – C.x) ) / d

となる。dが0の時に線分は平行となり、sとrがともに0～1の範囲のときに交差しているとみなせる。