定義
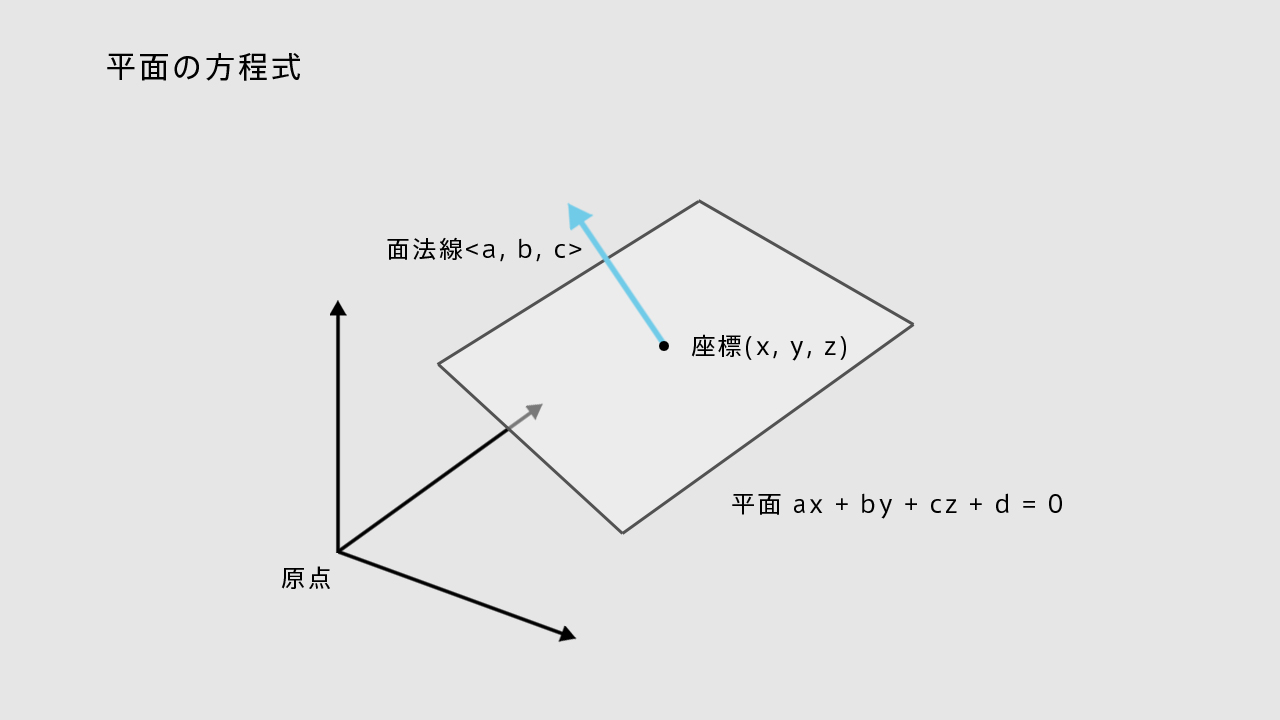
空間上の平面は平面式 ax + by + cz + d = 0 で定義できる。
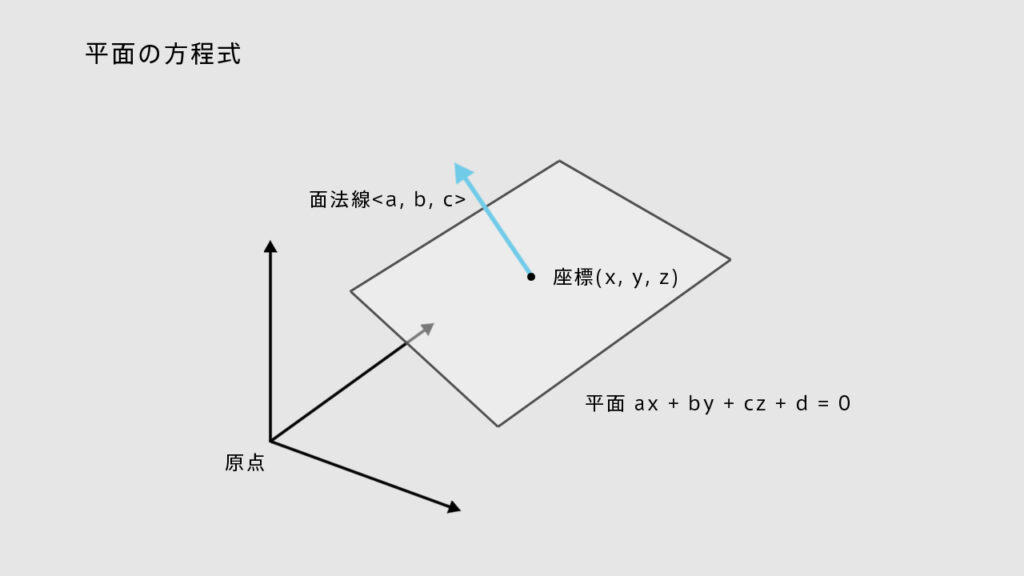
a, b, cは法線ベクトル、x, y, zは座標で、dは係数(内積)。法線ベクトルが正規化されている場合、dには原点から平面までの最短距離が入ることになる。
つまりベクトル(面法線)と座標があれば平面は定義できる(ある座標に接していて、ベクトル方向を向いている無限に広がる平面を想像するとよい)。
平面を定義するために三角形(または3頂点)が必要になる。三角形の面法線を三角形の頂点などから外積で導き、これがベクトル(a, b, c)になる。
座標(x, y ,z)には三角形の頂点座標のどれかを使う。これで平面式のd以外の要素がそろう。平面式は
a*x + b*y + c*z + d = 0
なのでd以外を右辺に移動させることでdの値を計算できる。
d = -(a*x + b*y + c*z)
軸に沿って平面にそろえる
ある頂点を定義された平面に沿ってY軸方向にそろえるとする。知りたい値は移動後のY座標になる(平面と交差する座標)。
まずは平面を定義してa, b, c, dを取得しておく。
平面式のy以外を右辺に移動させる。
a*x + b*y + c*z + d = 0
b*y = -(a*x + c*z + d)
y = -(a*x + c*z + d)/b;
xとzはわかっているのでa, b, c, dと一緒に右辺に代入すればyの値が得られる。x軸やz軸でも同じ要領で計算する。
ベクトルに沿って平面にそろえる
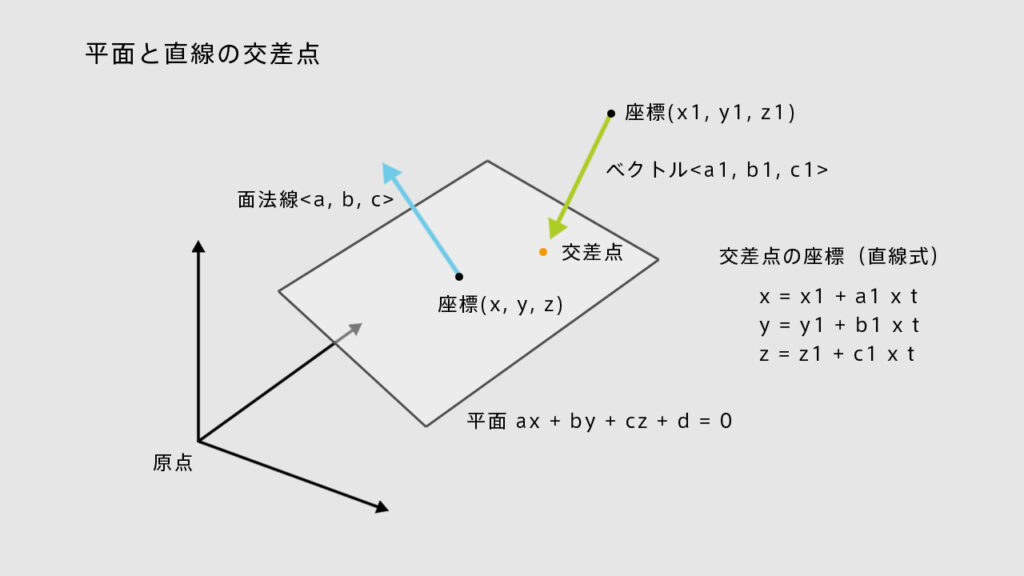
直線の式を使う。
通過点(x1, y1, z1)を通り、ベクトルが<a1, b1, c1>の直線の式は
x = x1 + a1 *t
y = y1 + b1 *t
z = z1 + c1 *t
となる。(t は任意の実数)
平面を定義した上で、平面の式に直線の式を代入してtを求める。
a*x + b*y + c*z + d = 0
x, y, zに直線式を代入する
a*(x1 + a1*t) + b*(y1 + b1*t) + c*(z1 + c1*t) + d = 0
これを展開していく
a*x1 + a*a1*t + b*y1 + b*b1*t + c*z1 + c*c1*t + d = 0
t以外を右辺に移動させていく
t*(a*a1 + b*b1 + c*c1) + a*x1 + b*y1 + c*z1 + d = 0
t = -(a*x1 + b*y1 + c*z1 + d)/(a*a1 + b*b1 + c*c1)
右辺の変数に値を代入して係数tを求めます。
整理すると
a, b, c :平面のベクトル
d :平面式の係数
a1, b1, c1 :直線のベクトル
x1, y1, z1 :移動させたい頂点の座標
初めの直線式にtの値を代入すれば、平面と交差する座標を求めることができます。
関数
// 平面と直線の交差座標を返す関数
vector rayIntersectPlane(vector planePos; vector planeNormal; vector origin; vector ray;)
{
float d = -(planeNormal.x * planePos.x + planeNormal.y * planePos.y + planeNormal.z * planePos.z);
float t = -(planeNormal.x * origin.x + planeNormal.y * origin.y + planeNormal.z * origin.z + d) / (planeNormal.x * ray.x + planeNormal.y * ray.y + planeNormal.z * ray.z);
return set(origin.x + ray.x * t, origin.y + ray.y * t, origin.z + ray.z * t);
}