線分の交差判定と交点の求め方

線分の交差判定について。まずは線分同士で判定をして、交差していることが確認できたら、直線同士の交点を計算する、という二段構えです。

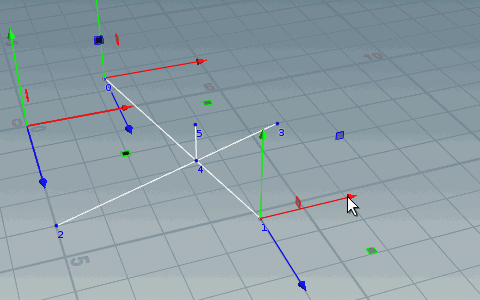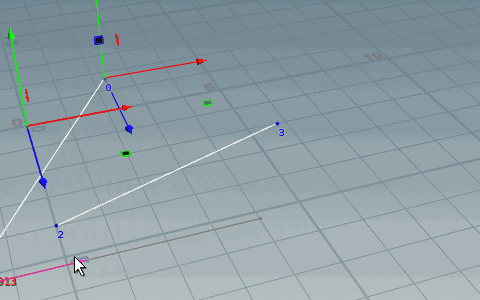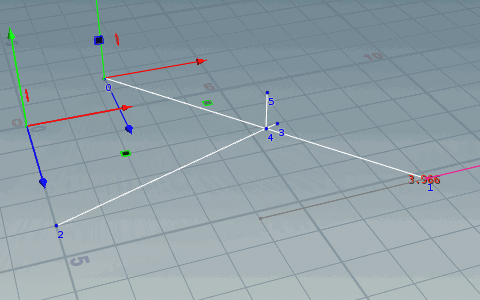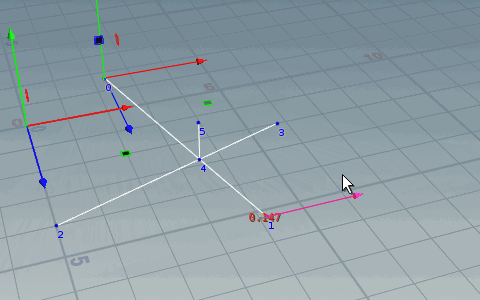
交差の判定

//
// 線分が交差しているかチェックする関数
//
int IsIntersectLine(vector p0; vector p1; vector p2; vector p3)
{
    int result = 0;
    
    // まずは線分ABが直線CDと交差しているか判定
    float ta = (p3.x - p2.x) * (p2.z - p0.z) + (p3.z - p2.z) * (p0.x - p2.x);
    float tb = (p3.x - p2.x) * (p2.z - p1.z) + (p3.z - p2.z) * (p1.x - p2.x);
     
    if(ta * tb < 0)
    {
        // 線分CDが直線ABと交差しているか判定
        float tc = (p1.x - p0.x) * (p0.z - p2.z) + (p1.z - p0.z) * (p2.x - p0.x);
        float td = (p1.x - p0.x) * (p0.z - p3.z) + (p1.z - p0.z) * (p3.x - p0.x);
         
        if(tc * td < 0)
        {
            result = 1;
        }
    }
    
    return result;
}

判別式if(ta * tb < 0)の符号を<=にするとギリギリ隣接している場合も交差している判別されます。

解説

線分ABと線分CDの交差を考えます。

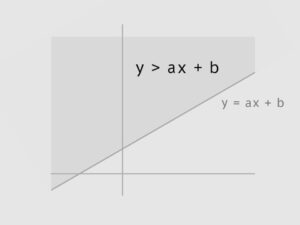
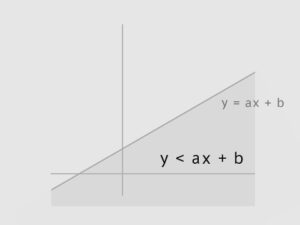
直線AB（y = ax + b）にたいして点C、Dがy > ax + bか、y < ax + bのどちら側にあるかで判定する。
点（x1, y1）、点（x2、y2）を通る直線の方程式は
(y2 – y1) / (x2 – x1) * (x – x1) = y – y1

この式を変形する。両辺に(x2 – x1)を掛ける
(x2 – x1) * y = (x2 – x1) * y1 + (y2 – y1) * x – (y2 – y1) * x1
(x2 – x1) * (y1 – y) + (y2 – y1) * (x – x1) = 0

この式のx、yに点C（x3、 y3）または点D（x4、y4）を代入する。解の符号を掛けてマイナスなら交差していると考える。（片方がプラス、片方がマイナスだと掛けてマイナスになる）

tc = (x2 – x1) * (y1 – y3) + (y2 – y1) * (x3 – x1)
td = (x2 – x1) * (y1 – y4) + (y2 – y1) * (x4 – x1)

tc * td < 0 なら交差している

これは直線ABと線分CDの交差なので、直線CDと線分ABの交差も調べる。

ta = (x4 – x3) * (y3 – y1) + (y4 – y3) * (x1 -x3)
tb = (x4 – x3) * (y3 – y2) + (y4 – y3) * (x2 -x3)

ta * tb < 0 なら交差。

ただ交差しているかの判定だけならここまで。

交点の計算

//
// 直線の交点を求める関数
//
vector CrossPoint(vector p0; vector p1; vector p2; vector p3)
{
    // 線分が交差していた場合、直線の交点座標を計算する
    float a1 = p0.z - p1.z;
    float b1 = p1.x - p0.x;
    float c1 = (p1.x - p0.x) * p0.z - (p1.z - p0.z) * p0.x;
     
    float a2 = p2.z - p3.z;
    float b2 = p3.x - p2.x;
    float c2 = (p3.x - p2.x) * p2.z - (p3.z - p2.z) * p2.x;
     
    float x = (c1 * b2 - c2 * b1) / (a1 * b2 - a2 * b1);
    float z = (a1 * c2 - a2 * c1) / (a1 * b2 - a2 * b1);
     
    // 交点座標のポイントを追加
    vector result = set(x, 0, z);
            
    return result;
}

解説

交差しているとわかったら、つぎに直線同士の交点を求める。
連立一次方程式なのでクラメールの公式を使う。

a1 * x + b1 * y = c1
a2 * x + b2 * y = c2

のとき

x = (c1 * b2 – c2 * b1) / (a1 * b2 – a2 * b1)
y = (a1 * c2 – a2 * c1) / (a1 * b2 – a2 * b1)

となる

点Ａ（x1、y1）、点Ｂ（x2、y2）の方程式
(y2 – y1) / (x2 – x1) * (x – x1) = (y – y1)

式を変形すると

(y1 – y2) * x + (x2 – x1) * y = (x2 – x1) * y1 – (y2 – y1) * x1

a1 = (y1 – y2)
b1 = (x2 – x1)
c1= (x2 – x1) * y1 – (y2 – y1) * x1

同じように点Ｃと点Ｄの式からa2、b2、c2を求める。