遠心加速度と片勾配

クルマが遠心力でカーブの外側に出ないように適切なバンク角をつける計算。

計算
実装
その他

計算

カーブのバンク角の計算から

\(θ=atan(\frac{a-gμ}{g+aμ})\)が傾斜の角度になる。

μ：摩擦係数
g：重力加速度（9.8m/s²）
R：曲率半径(m)
v：車両の速度（m/s）
a：遠心加速度\(\frac{v^2}{R}\)

実装

線形の曲率半径とハーフベクトルを事前に求めておく。ハーフベクトルは遠心力が働く方向の目安として利用する。

f@__radius：曲率半径
v@__h：ハーフベクトル

//
// 遠心力を計算し、
// ハーフベクトルの長さに掛ける
// RunOver:Points
//

int prim[] = pointprims(0, @ptnum);
float speed = prim(0, "designSpeed", prim[0]);  // 想定速度(km/h)
float f = prim(0, "friction", prim[0]); // 摩擦係数

// 時速を秒速へ（例：90kmh -> 25m/s）
float v = speed * 1000 / 60/60;
  
float g = 9.8;  // 重力(m/s^2)
float R = f@__radius;   // 曲率半径

// 曲率がある場合（＝直線でない）
if(R > 0)
{
    // 遠心力＝速度の二乗÷曲率半径
    float a = v * v / R;
    
    // 勾配の角度を求める
    float theta = atan((a-g*f)/(g+a*f));
    
    if(theta < 0) theta = 0;
    //f@__theta = degrees(theta);
    
    // 進行方向の行列
    matrix world = maketransform(@N, @up);
    matrix inverse = invert(world);
    
    // ハーフベクトルを原点に座標変換し、型勾配のベクトルと比較
    vector localH = v@__h * inverse;
    vector localLeft = set(cos(theta), sin(theta), 0);
    if(localH.x < 0) localLeft.y *= -1;
    
    vector left = localLeft * world;
    @up = cross(@N, left);
}

UPベクトルはSmooth SOP等で滑らかにする。

その他

国土交通省の道路構造令の計算式も内容は同じになっている。

参考：国土交通省道路構造令の各規定の解説 III-4.線形

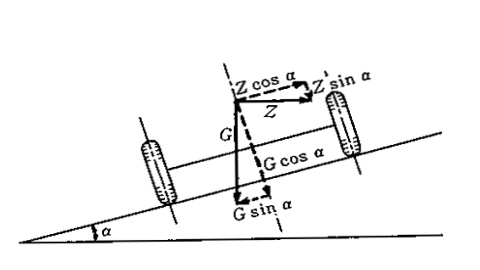
遠心力＝質量 * 速度² / 曲率半径

\(Z=\frac{G}{g}⋅\frac{v^2}{R}\)

Z：遠心力
v：速度(m/s)
g：重力加速度(9.81m/s^2)
G：クルマの総重量(N)
R：曲率半径(m)
f：路面とタイヤの摩擦係数

横滑りを生じさせない条件
\(Zcosθ-Gsinθ≦f(Zsinθ+Gcosθ)\)

式を変形してθにまとめる

\(Zcosθ – Gsinθ ≦ fZsinθ + fGcosθ\)
\(Zcosθ – fGcosθ ≦ fZsinθ + Gsinθ\)
\(cosθ(Z – fG) ≦ sinθ(fZ + G)\)
\(\frac{Z – fG}{fZ + G}≦\frac{sinθ}{cosθ}\)
\(\frac{Z – fG}{fZ + G}≦ tanθ\)
\(θ ≧ atan(\frac{Z – fG}{fZ + G})\)

θは\(atan(\frac{Z-fG}{fZ+G})\)以上の角度となる。

※1ニュートンは1kgの質量に1m/s²の加速度を発生させる力（単位：kg・ｍ/s^2）

質量が1トン＝1000kgの場合
総重量G = 1000kg * 9.81m/s² = 9810N