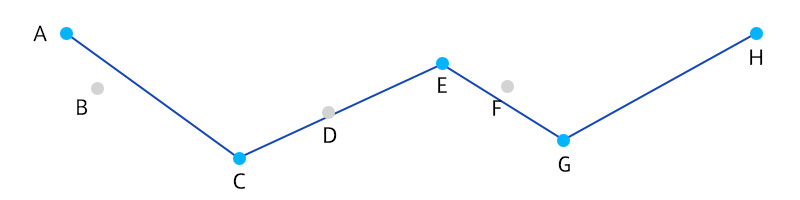
Douglas-Peuckerアルゴリズムに重みをつけてポリラインをリダクションします。
事前にf@weightアトリビュートを作っておき、0~1の値を設定しておきます。
0に近いほど削除されやすく、1ほど残りやすくなります。
node = hou.pwd()
geo = node.geometry()
# 許容距離
epsilon = 5
# ポイントクラス
class Point:
def __init__(self, index, pos, weight):
self.index = index
self.pos = hou.Vector3(pos)
self.weight = weight
# Douglas Peuckerのポリラインリダクション
def douglas_peucker(points, epsilon):
if len(points) < 3:
return points
start, end = points[0], points[-1]
max_distance = 0.0
index = 0
# 最大距離とそのインデックスを計算
for i in range(1, len(points) - 1):
distance = point_line_distance(points[i], start, end) * points[i].weight
if distance > max_distance:
max_distance = distance
index = i
# 許容距離を超える場合は再帰的に処理
if max_distance > epsilon:
left = douglas_peucker(points[:index + 1], epsilon)
right = douglas_peucker(points[index:], epsilon)
return left[:-1] + right
else:
return [start, end]
# 線分と点の最短距離
def point_line_distance(point, start, end):
if start.pos == end.pos:
return (point.pos - start.pos).length()
line_vec = (end.pos - start.pos).normalized()
point_vec = point.pos - start.pos
d = line_vec.dot(point_vec)
projection = start.pos + line_vec * d
dist = (point.pos - projection).length()
return dist
# Pointオブジェクトのリスト
points = []
index = 0
for pt in geo.points():
weight = pt.attribValue('weight')
points.append(Point(index, pt.position(), weight))
index += 1
# 簡略化されたポリラインを取得
simplified_points = douglas_peucker(points, epsilon)
# ポリラインを新しく生成する
geo.clear()
poly = geo.createPolygon(is_closed=False)
for i in range(len(simplified_points)):
pt = geo.createPoint()
pt.setPosition(simplified_points[i].pos)
poly.addVertex(pt)この後にPoint Wrangleをつないで不要なポイントを削除する。
// Run Over: Points
int pts[] = detail(0, "result");
if(len(pts) > 0 && find(pts, @ptnum) < 0)
removepoint(0, @ptnum);