ある関数f(x)のx=aからx=bまでの面積は、積分した関数F(x)から求まりますが、高校では説明されることもなく「そういうものなんだよ!」で済まされた気がします。腑に落ちないまま年月が流れ、最近になって急に思い出したので考えてみました。
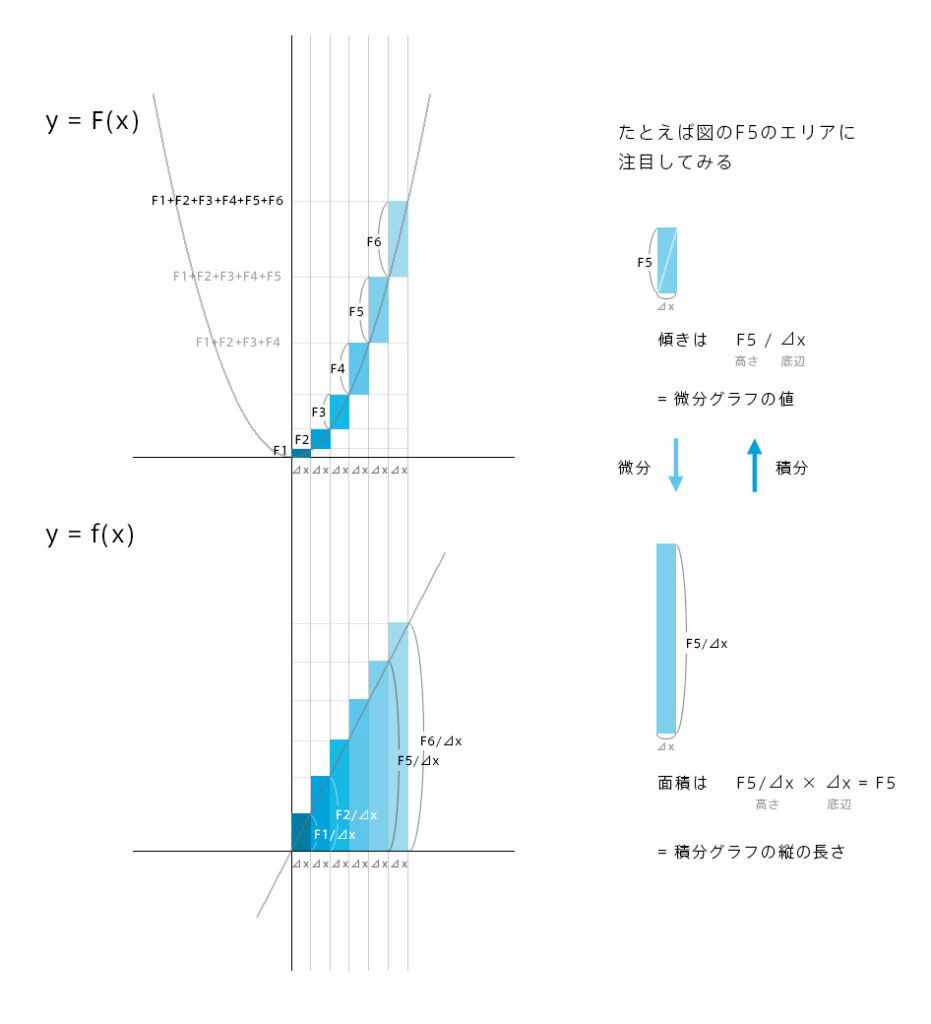
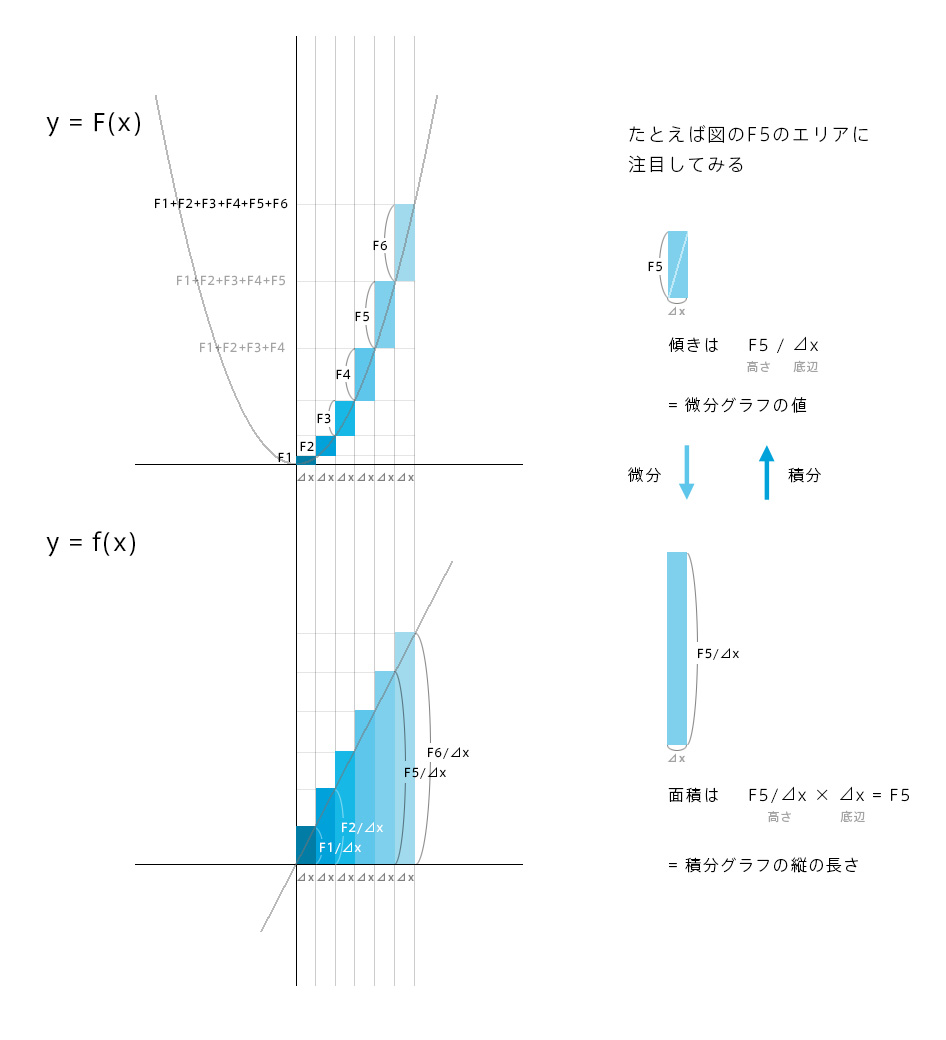
縦方向に超微小幅⊿xで細かく分割してひとつのエリアに注目してみるとその関係性がわかります。
微分グラフというのは傾きをグラフに表したものなので、積分グラフ(図の上のグラフ)の細かく区切った⊿x幅ごとの傾きの値(高さ÷底辺)がそのまま微分グラフ(図の下のグラフ)に落とし込まれます。微分グラフの縦の長さはもともと⊿xで割った値なので、横幅(⊿x)をかければまたもとの積分グラフの⊿x幅の縦の長さに戻るわけです。それがつまり底辺×高さの面積計算になっているということですね。
というわけで微分グラフは積分グラフの傾きを表したグラフ、積分グラフは微分グラフの面積を表したグラフになるというお互いの関係がわかると思います。