経度と緯度の角度でランダムの単位ベクトルを求めてみます。

経度は0~2π(0~360度)をランダムに選べば大丈夫ですが、緯度のほうはランダムに選ぶと問題があって、北極と南極の部分の表面積が赤道の部分に比べて小さくなるので、一様分布で乱数を振ると極に密集してしまうことになる。

なので、乱数に対して面積に比例した重みをつける必要がある。
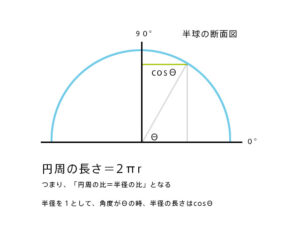
表面積の比は微分するイメージで、輪切りで細かく分割すると円周の長さの比になると考える。円周の長さの公式が2*πrなので、赤道から極までの円周の比はつまり半径の比になる。
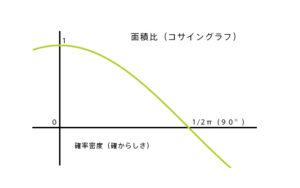
半径は三角比で求めるとcosΘになるので、つまり側面から見た輪切りの円周の長さはコサイングラフになる。
コサイングラフが面積比となり、面積比=確率とみなすので、グラフは確率密度と捉える。たとえば60°の角度のところはcos(60°)=0.5なので赤道cos(0°)=1.0に比べて面積が半分ということになる(赤道の半分ぐらいしか確率が発生しない)。
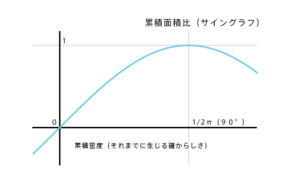
これらの確率の累積密度はコサイングラフを積分したサイングラフとなる。なので、乱数にアークサイン(サインの逆関数)を通せば重みのついた乱数が得られる。
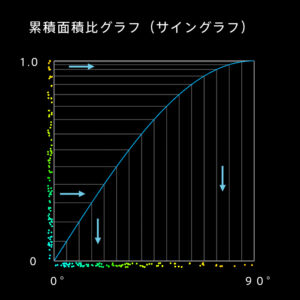
累積グラフの横軸を角度、縦軸を確率と見る。縦軸に乱数を振ると赤道(0)のほうのマスは広く、極の方(1.0)のマスは狭いので、赤道のほうがたくさん選ばれ、極の方は少なくなる。
コードにするとこのような感じになる
angleY = rand(0, PI*2)
angleX = asin(rand(-1, 1))
vector.Y = sin(angleX)
vector.X = cos(angleX) * cos(angleY)
vector.Z = cos(angleX) * sin(angleY)
どの方向にも偏りなく分布していますね。