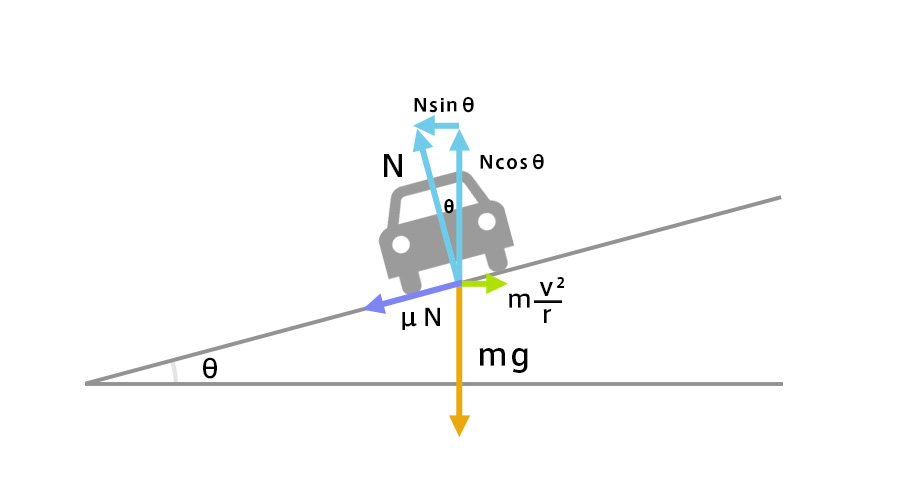
車両は道路の傾斜と遠心力によって支えられる。車が速く走るほど道路の傾斜を大きくしないと遠心力に負けてしまう。カーブの半径が大きいほど、傾きを少なくできる。
摩擦を考えない場合
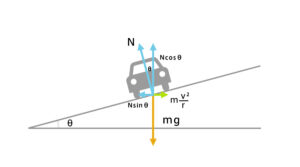
g:重力加速度(9.8m/s2)
m:質量(kg)
R:曲率半径(m)
v:車両の速度(m/s)
N:垂直抗力
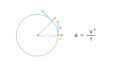
遠心加速度は
\(a=\frac{v^2}{R}\)
詳しくは、遠心力と遠心加速度
垂直抗力(道路から押し返される力)の水平成分は遠心力と、垂直成分は重力と釣り合う。
\(Nsinθ=m\frac{v^2}{R}\)・・・①
\(Ncosθ=mg\)・・・②
②を変形した\(N=\frac{mg}{cosθ}\)を①に代入する
\(mgtanθ=m\frac{v^2}{R}\)
\(gtanθ=\frac{v^2}{R}\)
\(tanθ=\frac{v^2}{gR}\)
\(θ=atan(\frac{v^2}{gR})\)
遠心加速度\(\frac{v^2}{R}\)をaとして計算した場合
\(θ=atan(\frac{a}{g})\)
となります。
摩擦を考える場合
摩擦係数μが加わる。
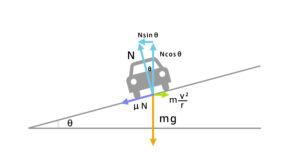
μ:摩擦係数
g:重力加速度(9.8m/s2)
m:質量(kg)
R:曲率半径(m)
v:車両の速度(m/s)
N:垂直抗力
垂直方向
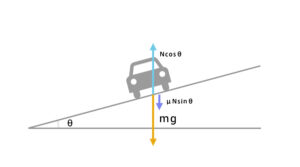
\(Ncosθ-μNsinθ=mg\)
\(N(cosθ-μsinθ)=mg\)
\(N=\frac{mg}{(cosθ-μsinθ)}\)・・・①
水平方向
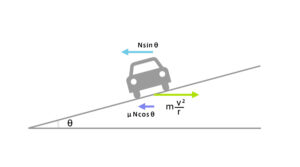
\(Nsinθ+μNcosθ=m\frac{v^2}{R}\)
\(N(sinθ+μcosθ)=m\frac{v^2}{R}\)・・・②
②に①を代入する
\(mg\frac{(sinθ+μcosθ)}{(cosθ-μsinθ)}=\frac{mv^2}{R}\)
\(gR\frac{(sinθ+μcosθ)}{(cosθ-μsinθ)}=v^2\)
θについて解く
\(gR(sinθ+μcosθ)=v^2(cosθ-μsinθ)\)
展開する
\(gRsinθ+gRμcosθ=v^2cosθ-v^2μsinθ\)
\(gRsinθ+v^2μsinθ=v^2cosθ-gRμcosθ\)
\(sinθ(gR+v^2μ)=cosθ(v^2-gRμ)\)
\(\frac{sinθ}{cosθ}=\frac{v^2-gRμ}{gR+v^2μ}\)
\(tanθ=\frac{v^2-gRμ}{gR+v^2μ}\)
\(θ=atan(\frac{v^2-gRμ}{gR+v^2μ})\)
μ=0なら摩擦がない場合の式と同じになる。
また、遠心加速度\(\frac{v^2}{R}\)をaとして計算した場合
\(θ=atan(\frac{a-gμ}{g+aμ})\)
となります。