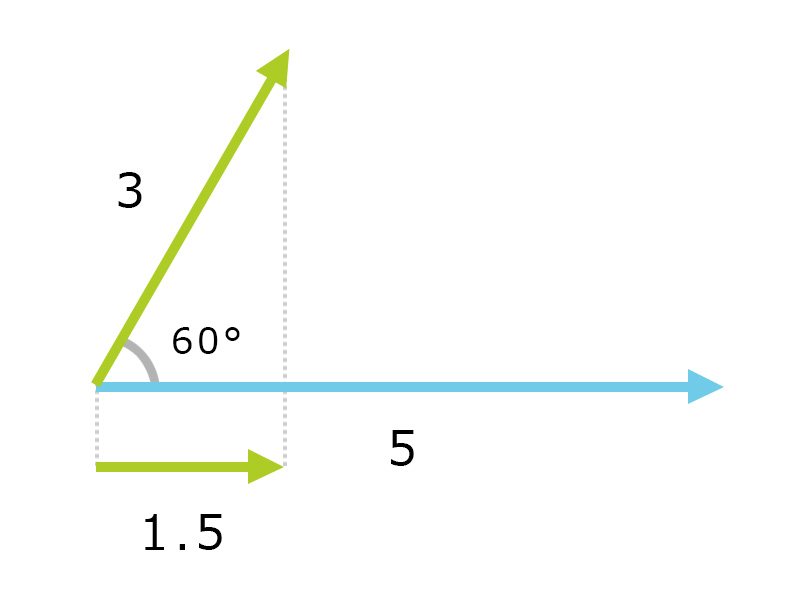
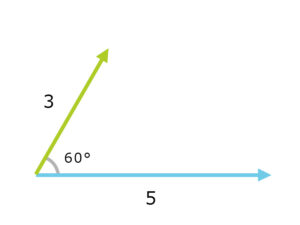
内積とは
片方のベクトルがもう片方のベクトルとともに行った仕事の量、と考えられる。
|a||b|cosΘ
60°の角度で別の方向を向いているベクトルがあるとする。長さ3のベクトルを長さ5のベクトルに投影すると、cos60°=0.5なの1.5の長さのベクトルになる。
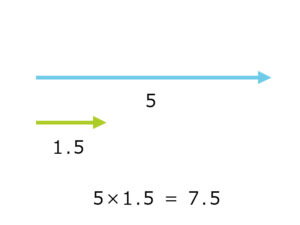
5と1.5を掛け合わせて、内積の値は7.5になる。片方のベクトルをもう片方のベクトルへ投影して、掛け合わせた値が内積。
ベクトル同士の内積で行われる計算
a = (2, 3, 0)、b = (2, 5, 0)の2つのベクトルの内積を求める場合
成分同士の積の和となる。内積=(x成分の積)+(y成分の積)+(z成分の積)
2×2 + 3×5 + 0×0 = 21
内積でできること
2つのベクトルの方向(前後関係)を調べる
ベクトル同士が同じ方向を向いているか否か、符号で判定できる。
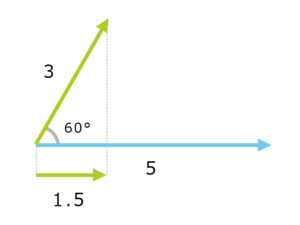
90°以下の場合は内積は5×1.5=7.5でプラスになり
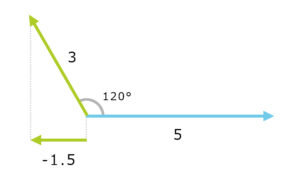
角度が90度以上ある場合は内積は5×-1.5=-7.5でマイナスになる
内積が1の時、全く同じ方向を向いている。
内積が0の場合は90度で直行している。
内積が-1の時は真逆の方向を向いている。
進んでいる方向に対して目標のポイントが前方にあるか、過ぎてしまったか、などの判定に使える。
角度を調べる
ベクトル同士の内積から角度を求めることが出来る。d = |a||b|cosΘなので、Θ=acos(d / |a||b|)
float angle = acos(dot(normalize(a), normalize(b)));内積は正規化したベクトルを使って計算する。これはアークコサイン関数が-1から1の範囲の値しか取らないため。