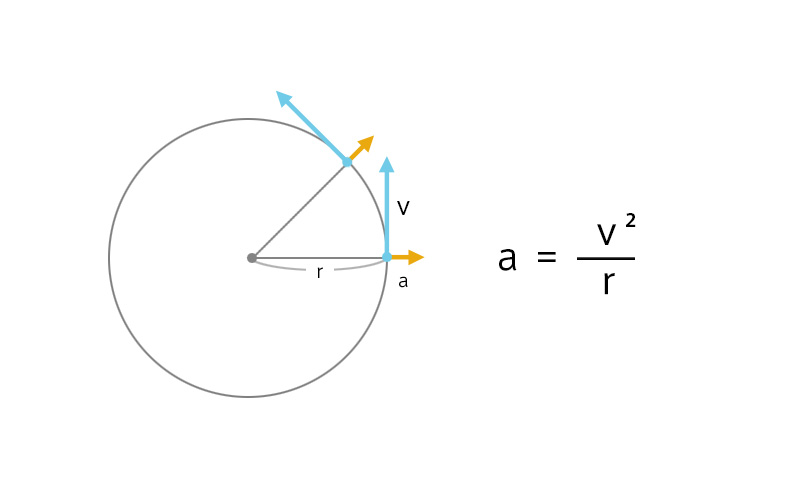遠心加速度
\(a=\frac{v^2}{r}\)
遠心加速度の単位は(m/s2)
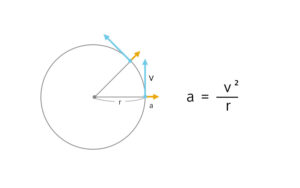
遠心加速度(m/s2) = 速度(m/s)2 / 曲率半径(m)
※遠心力は実際に存在している力ではなく、運動中の物体側で感じる見かけの力。
\(a=\frac{v^2}{r}\)の導出
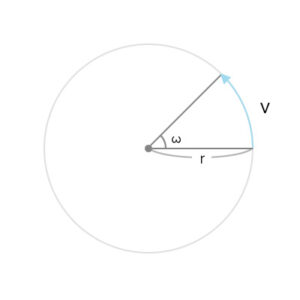
角速度の式。単位はラジアン。
\(v=rω\)・・・①
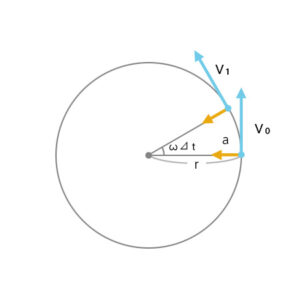
向心加速度aを求める。
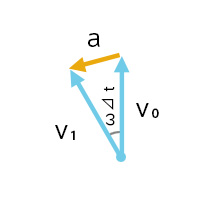
微小時間Δtにおける弧は直線になる、と考えると、角度ωΔtにおける弧の長さはvωΔtとなる。
\(a=\frac{vωdt}{dt}=vω\)・・・②
①の\(v=rω\)を変形した\(ω=\frac{v}{r}\)を②に代入する。
\(a=\frac{v^2}{r}\)
向心力加速度の式が求まる。
遠心力は向心力の反対で、力の大きさが等しく向きが反対になる。
遠心力
\(F=m\frac{v^2}{r}\)
遠心力(N)= 質量(kg)* 遠心加速度(m/s2)
遠心力の単位は(N)
遠心加速度に質量(kg)を掛けたものが遠心力(kg・m/s2)となる。なので遠心力は質量に比例する。
例題
カーブを曲がるクルマ
1トンのクルマが時速72km(秒速20m)で曲率半径100mのカーブを曲がる時の遠心力を求める
1000(kg) * 20(m/s)2 / 100(m) = 4000(N)
この時の遠心加速度は20(m)2 / 100(m) = 4(m/s2)
宇宙コロニー
直径5kmの円筒型の回転宇宙コロニーで9.81m/s^2の遠心加速度(人工重力)を発生させるために回転させる速度を求める
遠心加速度a(m/s2)
速度v(m/s)
半径r(m)
\(a=\frac{v^2}{r}\)なので
\(v=\sqrt{ar}\)
\(v=\sqrt{9.81\times2500}\)
\(v=156.6\)
回転させる速度は156.6(m/s)になる。(時速にすると563.7km/h)