バーチカル曲線

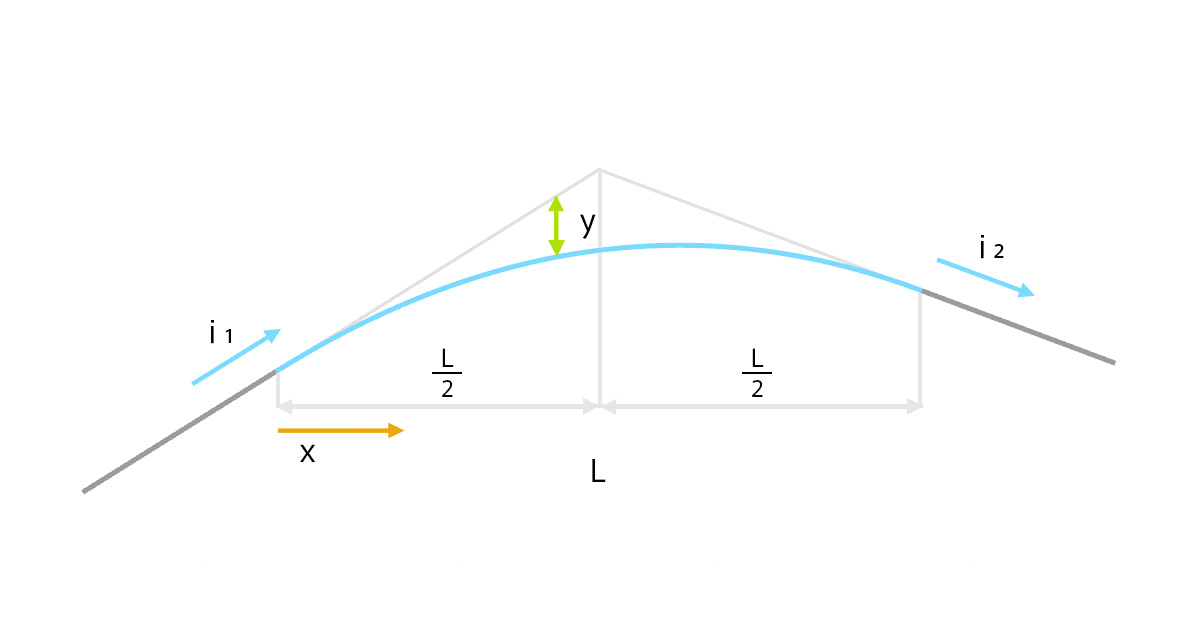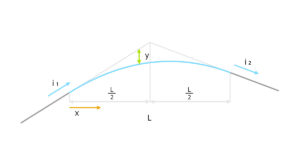
土木で使われているバーチカル曲線の計算について。

縦断曲線とは

道路や鉄道の縦断方向の勾配変化を滑らかするために設計される曲線。直線勾配の変更点に用いられる。勾配の急激な変化を緩和することで、車両が衝撃を受けにくくなり、乗り心地が向上する。また、視界の変化も緩やかになるため安全運転に寄与する。

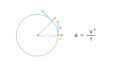
\(y=\frac{1}{2}rx^2\)・・・①

放物線を表す式。rが重力なら自由落下を表す式になる。

\(r = \frac{i_1-i_2}{L}\)・・・②

i₁：始点の勾配
i₂：終点の勾配
L：水平長(m)

単位距離あたりの勾配（傾き）の変化率を示している。

例：\(i_1= 4%\)、\(i_2= -2％\)で長さLが200mの場合

\(\frac{0.04-(-0.02)}{200}=0.003\)

1mあたりの勾配は0.3%になる。

放物線の式①に曲率の式②を代入する

\(y = \frac{(i_1-i_2)}{2L}x^2\)

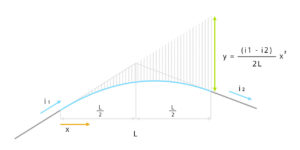
i₁：始点の勾配
i₂：終点の勾配
L：水平長(m)
x：始点からの水平距離(m)
y：補正前と後の高さの差(m)

ここで注意したいのは、yは高さではなく放物線の縦方向の長さ。

始点からの直線から放物線の値だけ変化した座標を曲線とする。始点から交点、交点から終点までの距離を等しくすることで、傾きや高さのつじつまが合って終点の直線につながる。

放物線の高さの式にするなら

\(y = i_1x-\frac{(i_1-i_2)}{2L}x^2\)

となる。カーブが始まる座標が始点になる。