とあるデザイナーのテクニカルノート

数学ノート

クロソイド曲線

公開 更新

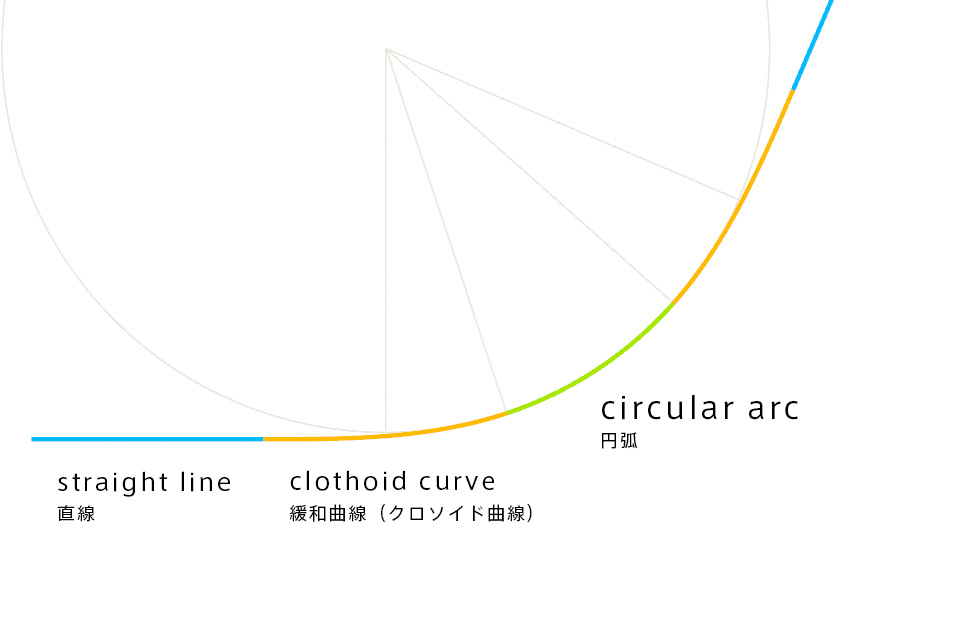
クロソイド曲線とは

クロソイド曲線は道路や鉄道、ローラーコースター等で使われている曲線で、人体への負担を軽減し、乗り心地を向上させる効果がある。この曲線は、直線から円弧に移行する際に、急激な方向転換を避けるために使用されている。

クロソイド曲線は曲率を一定の割合で増加させて描かれる。

直線から円にいきなり進入すると急にハンドルを大きく切る必要が生じ、事故のリスクが高まる可能性がある。クロソイド曲線を挟むことでハンドル操作が徐々に行えるようになり、スムーズな移行が可能になる。事故削減効果が顕著で、多くの分野で積極的に使われるようになった。

公式と計算

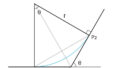
クロソイドの公式 R⋅L=A2R⋅L=A^2 τ=L2Rτ=\frac{L}{2R}

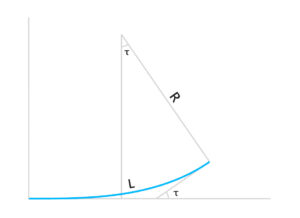
R：円の半径 L：クロソイド曲線長 A：クロソイドパラメータ τ：接線角（タウと読む）

２つの要素を決めると残りが決まる

公式R⋅L=A2R⋅L=A^2とτ=L2Rτ=\frac{L}{2R}から、RとLが決まれば残りのAとτが決まり、AとLが決まればRとτが決まる。先に２つを決めると残りが自動的に決まる、という関係性になっている。

RとLから A（パラメータ）はA=R⋅LA=\sqrt{R⋅L}で求まる。 τ （接線角）はτ=L2Rτ=\frac{L}{2R}で求まる。

例：R=10m、L=12mのときAは10.9545、τは34.3775°

AとLから R（半径）はR=A2LR=\frac{A^2}{L}から求まる。 τ （接線角）はτ=L2Rτ=\frac{L}{2R}で求まる。

AとRから L（曲線長）はL=A2RL=\frac{A^2}{R}から求まり τ （接線角）はτ=L2Rτ=\frac{L}{2R}で求まる。

τとRから A（パラメータ）はA=R2τA=R\sqrt{2τ}で求まる。 L（曲線長）はL=A2RL=\frac{A^2}{R}で求まる。

τとLから R（半径）はR=L2τR=\frac{L}{2τ}から求まる。 A（クロソイドパラメータ）はA=R⋅LA=\sqrt{R⋅L}で求まる。

τとAから R（半径）はR=A2τR=\frac{A}{\sqrt{2τ}}から求まる。 L（曲線長）はL=A2RL=\frac{A^2}{R}で求まる。

R⋅L=A2R⋅L=A^2

クロソイド曲線は曲率を一定の割合で増加させて描かれる曲線で、曲率半径Rと始点からの曲線長Lの積は一定となる。

曲率は1R\frac{1}{R}なので、cを比例定数とすると以下の式が成り立つ。

1R=c×L\frac{1}{R}=c\times L

曲率と距離が比例関係になっている。これを変形すると

R⋅L=1cR⋅L=\frac{1}{c}

となり、1c\frac{1}{c}をA2A^2に置き換えたものがクロソイドの基本式R⋅L=A2R⋅L=A^2になる。

Aはクロソイドパラメータと呼ばれ、曲率の増加度をあらわす。Aの値が大きいほど与えられたLに対して曲率半径Rが大きくなり、緩やかな曲線になる。

τ=L2Rτ=\frac{L}{2R}

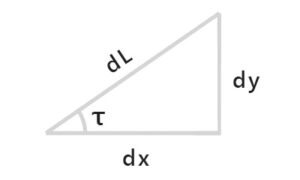
曲線長LがdLだけ微量変化したとすれば、x, y, τもdx, dy, dτだけ微量変化する。

dτdL=1R\frac{dτ}{dL}=\frac{1}{R}・・・① dx=dL⋅cosτdx=dL·cosτ・・・② dy=dL⋅sinτdy=dL·sinτ・・・③

①を変形したdL=R⋅dτdL=R·dτにR=A2LR=\frac{A^2}{L}を代入すると dL=A2L⋅dτdL = \frac{A^2}{L}⋅dτ・・・④

④を積分すると LdL=A2⋅dτLdL=A^2⋅dτ 12L2=A2τ\frac{1}{2}L^2=A^2τ L2=2A2τL^2=2A^2τ・・・⑤

これをτについて解くと τ=L22A2τ=\frac{L^2}{2A^2} となり、基本式からA2=RLA^2=RLを代入すると τ=L22RLτ=\frac{L^2}{2RL} τ=L2Rτ=\frac{L}{2R}・・・⑥ が得られる。

X, Yの導出

②、③にそれぞれ④を代入し、さらに⑤よりL=A2τL=A\sqrt{2τ}を代入して２つの微分方程式にする

dx=dLcosτ=A2Lcosτdτ=A2τcosτdτdx = dLcosτ = \frac{A^{2}}{L}cosτdτ = \frac{A}{\sqrt{2τ}}cosτdτ

dy=dLsinτ=A2Lsinτdτ=A2τsinτdτdy = dLsinτ = \frac{A^{2}}{L}sinτdτ = \frac{A}{\sqrt{2τ}}sinτdτ

A2\frac{A}{\sqrt{2}}を前に出して積分する

x=A2∫0τcosττdτx = \frac{A}{\sqrt{2}}\int_{0}^{τ} \frac{cosτ}{\sqrt{τ}}dτ・・・⑦

y=A2∫0τsinττdτy = \frac{A}{\sqrt{2}}\int_{0}^{τ} \frac{sinτ}{\sqrt{τ}}dτ・・・⑧

sinτ、cosτをマクローリン展開する

cosτ=1−τ22!+τ44!−τ66!+⋅⋅⋅cosτ=1-\frac{τ^2}{2!}+\frac{τ^4}{4!}-\frac{τ^6}{6!}+···

sinτ=τ−τ33!+τ55!−τ77!+⋅⋅⋅sinτ=τ-\frac{τ^3}{3!}+\frac{τ^5}{5!}-\frac{τ^7}{7!}+···

⑦の右辺からA2\frac{A}{\sqrt{2}}を除いたものを整理していく

∫0τcosττdτ=∫0τ1τ(1−τ22!+τ44!−τ66!+⋅⋅⋅)dτ\int_{0}^{τ} \frac{cosτ}{\sqrt{τ}}dτ = \int_{0}^{τ} \frac{1}{\sqrt{τ}}\left( 1-\frac{τ^2}{2!}+\frac{τ^4}{4!}-\frac{τ^6}{6!}+··· \right)dτ

=∫0τ(τ−12−12!τ2−12+14!τ4−12−16!τ6−12+⋅⋅⋅)dτ=\int_{0}^{τ}\left( τ^{-\frac{1}{2}} - \frac{1}{2!}τ^{2-\frac{1}{2}} + \frac{1}{4!}τ^{4-\frac{1}{2}} - \frac{1}{6!}τ^{6-\frac{1}{2}} +··· \right)dτ

=∫0τ(τ−12−12!τ32+14!τ72−16!τ112+⋅⋅⋅)dτ=\int_{0}^{τ}\left( τ^{-\frac{1}{2}} - \frac{1}{2!}τ^{\frac{3}{2}} + \frac{1}{4!}τ^{\frac{7}{2}} - \frac{1}{6!}τ^{\frac{11}{2}} +··· \right)dτ

=2τ12−12!×25τ52+14!×29τ92−16!×213τ132+⋅⋅⋅=2τ^{\frac{1}{2}} - \frac{1}{2!}\times\frac{2}{5}τ^{\frac{5}{2}} + \frac{1}{4!}\times\frac{2}{9}τ^{\frac{9}{2}} - \frac{1}{6!}\times\frac{2}{13}τ^{\frac{13}{2}} +···

=2τ12(1−12!×5τ2+14!×9τ4−16!×13τ6+…)=2τ^{\frac{1}{2}}\left( 1-\frac{1}{2!\times5}τ^2+\frac{1}{4!\times9}τ^4-\frac{1}{6!\times13}τ^6+…\right)

=2τ(1−12!×5τ2+14!×9τ4−16!×13τ6+…)=2\sqrt{τ}\left( 1-\frac{1}{2!\times5}τ^2+\frac{1}{4!\times9}τ^4-\frac{1}{6!\times13}τ^6+…\right)

⑧の右辺からA2\frac{A}{\sqrt{2}}を除いたものを整理していく

∫0τsinττdτ=∫0τ1τ(τ−τ33!+τ55!−τ77!+⋅⋅⋅)dτ\int_{0}^{τ} \frac{sinτ}{\sqrt{τ}}dτ = \int_{0}^{τ} \frac{1}{\sqrt{τ}}\left( τ-\frac{τ^3}{3!}+\frac{τ^5}{5!}-\frac{τ^7}{7!}+··· \right)dτ

=∫0τ(τ−τ523!+τ925!−τ1327!+⋅⋅⋅)dτ=\int_{0}^{τ} \left( τ-\frac{τ^{\frac{5}{2}}}{3!}+\frac{τ^{\frac{9}{2}}}{5!}-\frac{τ^{\frac{13}{2}}}{7!}+··· \right)dτ

=23τ32−23!×7τ72+25!×11τ112−27!×15τ152+⋅⋅⋅=\frac{2}{3}τ^{\frac{3}{2}}-\frac{2}{3!\times7}τ^{\frac{7}{2}}+\frac{2}{5!\times11}τ^{\frac{11}{2}}-\frac{2}{7!\times15}τ^{\frac{15}{2}}+···

=23τ32(1−τ23!×73+τ45!×113−τ67!×153+⋅⋅⋅)=\frac{2}{3}τ^{\frac{3}{2}}\left( 1-\frac{τ^2}{\frac{3!\times7}{3}}+\frac{τ^4}{\frac{5!\times11}{3}}-\frac{τ^6}{\frac{7!\times15}{3}}+···\right)

=23ττ(1−τ23!×73+τ45!×113−τ67!×153+…)=\frac{2}{3}τ\sqrt{τ}\left( 1-\frac{τ^2}{\frac{3!\times7}{3}}+\frac{τ^4}{\frac{5!\times11}{3}}-\frac{τ^6}{\frac{7!\times15}{3}}+…\right)

まとめると以下の結果になる。（級数の···以下の値は小さいので無視してよい）

x=A2×2τ(1−12!×5τ2+14!×9τ4−16!×13τ6+⋅⋅⋅)x=\frac{A}{\sqrt{2}}\times2\sqrt{τ}\left( 1-\frac{1}{2!\times5}τ^2+\frac{1}{4!\times9}τ^4-\frac{1}{6!\times13}τ^6+···\right)

y=A2×23ττ(1−τ23!×73+τ45!×113−τ67!×153+⋅⋅⋅)y=\frac{A}{\sqrt{2}}\times\frac{2}{3}τ\sqrt{τ}\left( 1-\frac{τ^2}{\frac{3!\times7}{3}}+\frac{τ^4}{\frac{5!\times11}{3}}-\frac{τ^6}{\frac{7!\times15}{3}}+···\right)

これでAとτの値を使って曲線のX,Y座標が計算できるようになった。

曲線の描画

半径Rが10、τが45°のクロソイド曲線を描画する。

// 
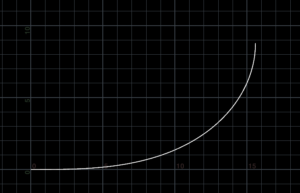
// クロソイド曲線の描画
// Run Over: Detail
//

// クロソイド曲線のX成分を求める関数(tauとAから)
function float clothoid_x(float tau; float A)
{
    return A / sqrt(2) * 2 * sqrt(tau) * (1 - (pow(tau, 2) / 10.0) + (pow(tau, 4) / 216.0) - (pow(tau, 6) / 9360.0));
}

// クロソイド曲線のY成分を求める関数
function float clothoid_y(float tau; float A)
{
    return A / sqrt(2) * (2/3.0) * sqrt(tau) * tau * (1 - (pow(tau, 2) / 14.0) + (pow(tau, 4) / 440.0) - (pow(tau, 6) / 25200.0) );
}

float R = 10;
float tau = radians(45);
float A = R * sqrt(2*tau);

// 原点にクロソイド曲線を描画する
int prim = addprim(0, "polyline");
int num = 100; // サンプルポイント数
for(int i = 0; i < num; i++)
{
    float t = tau / float(num-1) * i;
    
    float x = clothoid_x(t, A);
    float y = clothoid_y(t, A);
    
    vector pos = set(x, y, 0);
    
    int pt = addpoint(0, pos);
    addvertex(0, prim, pt);
}

三角関数微分曲線積分

← 記事一覧へ