円弧の半径と角度を求める

公開 2022-11-02 01:00更新 2025-05-21 00:15

矢高と弧長から求める

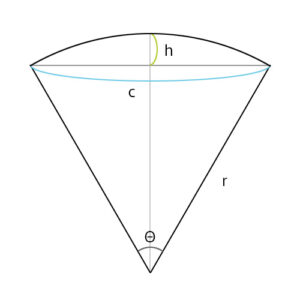
矢高(h)と弦(c)から半径(r)と角度(θ)を計算する。ピタゴラスの定理で求まる。

半径を求める

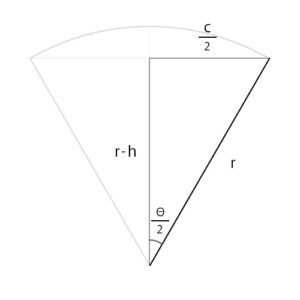
$(r - h)^2 + (\frac{c} {2})^2 = r^2$

rにまとめると

$h^2 - 2rh + (\frac{c}{2})^2 = 0$

$2rh = h^2+\frac{c^2}{4}$

$r = \frac{\frac{c^2}{4} + h^2}{2h}$

角度を求める

半径が求まると、θも求まる。

$\frac{c}{2} = rsin(\frac{θ}{2})$なので

$sin(\frac{θ}{2}) = \frac{c}{2r}$

$θ＝2 asin(\frac{c}{2r})$

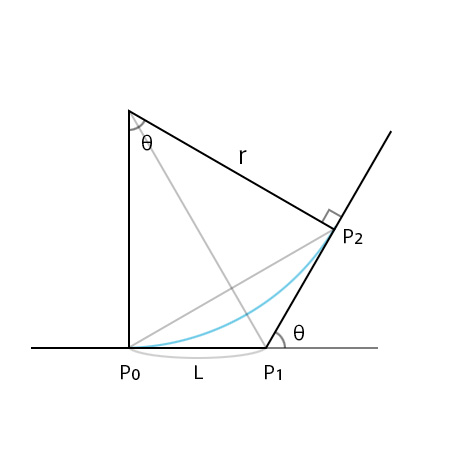
2辺から求める

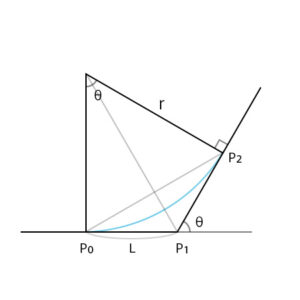
中心角θは２つの辺が成す角度となるので、それぞれのベクトルの内積からアークコサインで求める。

$θ=acos(dot(P_1-P_0, P_2-P_1))$

半径rは

$tan(\frac{θ}{2})=\frac{L}{r}$なので

$r=\frac{L}{tan(\frac{θ}{2})}$

となる。

三角関数円弧