万有引力と第一宇宙速度

万有引力の法則
1. 重力加速度の式
2. 重力加速度\(9.8m/s^2\)確認する
衛星と第一宇宙速度
例題
1. ISSの速度を求める
2. 月の速度を求める

万有引力の法則

重力加速度の式

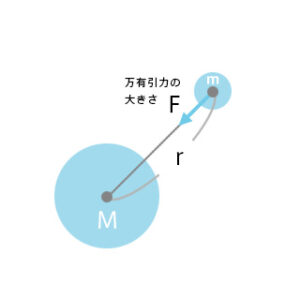
万有引力の公式

\(F=G\frac{Mm}{r^2}\)

G：万有引力定数
M：質量M
m：質量m
r：距離

万有引力定数は
\(G=6.67\times10^{-11}Nm^2/kg^2\)

運動方程式を立てて代入する
\(F=ma\)

重力加速度なのでmaはmgとする
\(mg=G\frac{Mm}{r^2}\)

\(g=\frac{GM}{r^2}\)・・・重力加速度の式となる。

重力加速度\(9.8m/s^2\)確認する

地球の質量5.972 x 10²⁴kg、半径6,371kmを使って計算すると

\(g = \frac{GM }{r^2}\)

\(\frac{(6.67\times10^{-11}) \times (5.972 \times 10^{24})}{6371000^{2}} = 9.819943\)

となり、重力加速度9.8m/s²が導き出される。

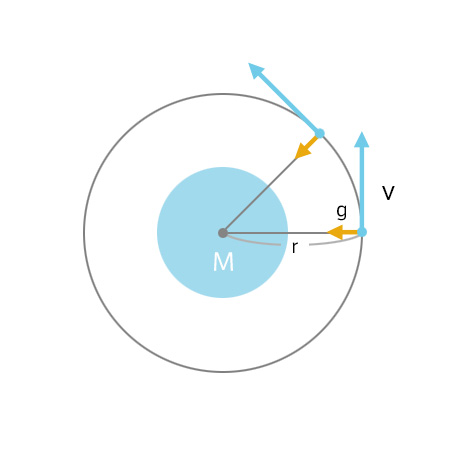
衛星と第一宇宙速度

ISS（国際宇宙ステーション）が地球を回っているのはエンジンを噴かして飛んでいるわけではなく、地球に落ちない速度で動いているから。このギリギリ落ちない速度を第一宇宙速度といい、円運動を理解することで計算できるようになります。

角速度

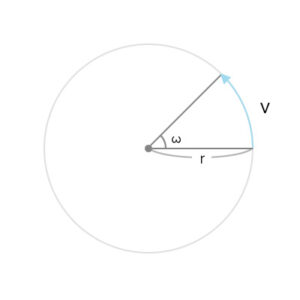
\(v=rω\)・・・①
（ωの単位はラジアン）

はじめに角速度。一定の半径で回り続ける場合、弧の長さは角度（ラジアン）×半径となる。この場合、弧の長さが速度になります（弧度法）。

向心力

つぎに向心力。速度ベクトルが円運動をするために必要な加速度を求める。この中心に働く加速度がないと速度ベクトルはまっすぐ進むことになる。ハンドルを切って横方向に力を加えるようなイメージをするといいかもしれません。求め方は微小時間で考えるとわかりやすくなります。

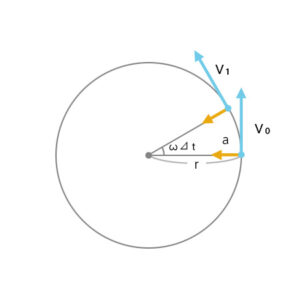
aは加速度ベクトル。

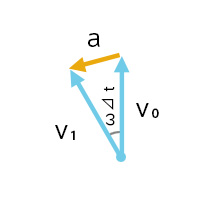
微小時間Δtにおける弧は直線になると考えて角度ωΔtにおける弧の長さはvωΔtとなる。

\(a=\frac{vωdt}{dt}=vω\)
①の\(v=rω\)を変形した\(ω=\frac{v}{r}\)代入することで

\(a=\frac{v^2}{r}\)・・・②

向心加速度の式を得ることが出来る。

第一宇宙速度

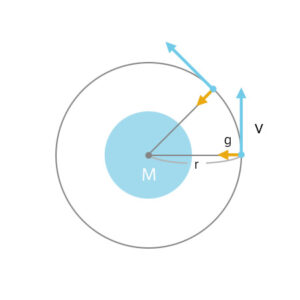
重力加速度の式\(g=\frac{GM}{r^2}\)に向心力の式\(a=\frac{v^2}{r}\)を代入する

\(\frac{v^2}{r}=\frac{GM}{r^2}\)

\(v=\sqrt{\frac{GM}{r}}=\sqrt{gr}\)

重力加速度と向心力の式をまとめると円運動をするための速度、つまり第一宇宙速度の式になる。

例題

ISSの速度を求める

高度400kmのISSに必要な速度は7.642km/sになります。ちなみに高度400kmにおける重力加速度は8.693m/s²となり、地上より少し軽い。

import math

# 重力を計算する関数
def CalcGravity(G, M, r):
    return G * M / pow(r, 2)

# 第一宇宙速度を計算する関数
def CalcFirstCosmicVelocity(G, M, r):
    return math.sqrt(G * M / r)
    
# 万有引力定数
G = 6.67428 * pow(10, -11)

# 地球の質量(kg)
massEarth = 5.972 * pow(10, 24);

# 地球の半径(m)
radiusEarth = 6371000

# ISSにかかる重力を調べる（ISSの高度＝400km）
h = 400000
g = CalcGravity(G, massEarth, radiusEarth + h);
print(str(g) + ' m/s^2')
# 8.69397913787899 m/s^2

# ISSに必要な速度を調べる
v = CalcFirstCosmicVelocity(G, massEarth, radiusEarth + h)
print(str(v) + ' m/s')
# 7672.478917701804 m/s

月の速度を求める

月が地球へ落ちないために必要な速度は、地球からの距離が384,400 kmなので1.018km/sになります。

import math

# 第一宇宙速度を計算する関数
def CalcFirstCosmicVelocity(G, M, r):
    return math.sqrt(G * M / r)
    
# 万有引力定数
G = 6.67428 * pow(10, -11)

# 地球の質量(kg)
massEarth = 5.972 * pow(10, 24);

# 月が周回するための速度を求める（地球からの距離384,400 km）
h = 384400000
v = CalcFirstCosmicVelocity(G, massEarth, h)
print(str(v) + ' m/s')
# 1018.2875200380001 m/s