クラメルの公式を図形的に視覚化してみます。
クラメルの公式とは
\(2x + y = 8\)
\(x + 3y = 9\)
といった連立方程式を代入や消去法を使わずに
\(x = \frac{(8\times3 – 1\times9)}{(2\times3 – 1\times1)}= 3\)
\(y = \frac{(8\times1 – 2\times9)}{(1\times1 – 2\times3)} = 2\)
と係数の四則演算だけで求めることが出来る便利な公式です。今回はわかりやすさを考えて二次元のクラメールの式で解説していきます。
クラメールの公式
\(ax+by=e\)
\(cx+dy=f\)
\(\begin{bmatrix}a \\c \\ \end{bmatrix}x +
\begin{bmatrix}b \\d \\ \end{bmatrix}y =
\begin{bmatrix}e \\f \\ \end{bmatrix}\)
\(\begin{bmatrix}a \\c \\ \end{bmatrix}=\vec{A},\begin{bmatrix}b \\d \\ \end{bmatrix}=\vec{B},\begin{bmatrix}e \\f \\ \end{bmatrix}=\vec{C}\)と置くと
\(x=\frac{det(\vec{C},\vec{B})}{det(\vec{A},\vec{B})}\)
\(y=\frac{det(\vec{C},\vec{A})}{det(\vec{B},\vec{A})}\)
これがクラメールの公式です。detという式を使っていますが、これはdeterminant(行列式)という意味になります。
行列式とは
\(det\begin{vmatrix}a & b \\c & d \\ \end{vmatrix}=ad-bc\)
まずクラメルの公式に使われている「行列式」が何を意味しているのかということから説明します。答えを先に書いてしまうとこれが意味するものは2つのベクトルが成す平行四辺形の面積です。
図形にして見ていくと、
行列式の\(ad-bc\)は\(\vec{A}=\begin{bmatrix}a \\c \\ \end{bmatrix}\)と\(\vec{B}=\begin{bmatrix}b \\d \\ \end{bmatrix}\)の成す平行四辺形の面積を意味している。
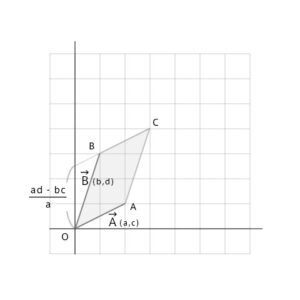
BCを通る直線は\(y=\frac{c}{a}(x-b)+d=\frac{c}{a}x+\frac{ad-bc}{a}\)
なので直線BCのY切片は\(\frac{ad-bc}{a}\)
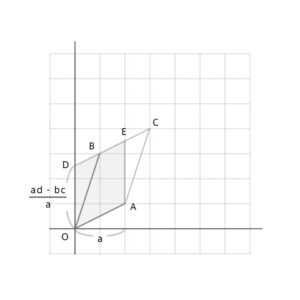
平行四辺形OACBを等積移動した平行四辺形OAEDの面積は
\(\frac{ad-bc}{a}\times a=ad-bc\)となる。
ベクトルの成分同士を掛け合って引き算することで上手く平行四辺形の面積になっていることがわかると思います。クラメールの公式はこの考え方を基本に成り立っています。
連立方程式を図形化してみる
連立方程式はベクトルの形にしてみると、平行四辺形の関係になります。
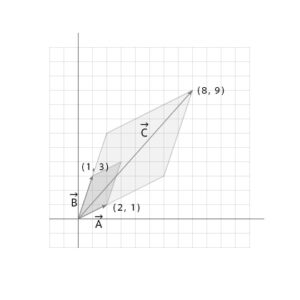
\(2x + y = 8\)
\(x + 3y = 9\)
\(\begin{bmatrix}2 \\1 \\ \end{bmatrix}x +
\begin{bmatrix}1 \\3 \\ \end{bmatrix}y =
\begin{bmatrix}8 \\9 \\ \end{bmatrix}\)
\(\begin{bmatrix}2 \\1 \\ \end{bmatrix}=\vec{A},
\begin{bmatrix}1 \\3 \\ \end{bmatrix}=\vec{B},
\begin{bmatrix}8 \\9 \\ \end{bmatrix}=\vec{C}\)
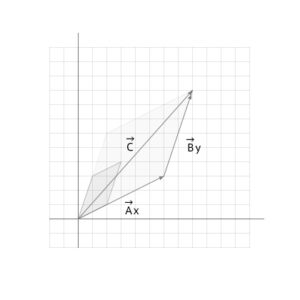
\(Ax+By=C\)
ベクトルの式にすると図のようなイメージになる。
クラメールの公式を分解していく
あらためて公式を見てみます。
クラメールの公式
\(ax+by=e\)
\(cx+dy=f\)
\(\begin{bmatrix}a \\c \\ \end{bmatrix}x +
\begin{bmatrix}b \\d \\ \end{bmatrix}y =
\begin{bmatrix}e \\f \\ \end{bmatrix}\)
\(\begin{bmatrix}a \\c \\ \end{bmatrix}=\vec{A},\begin{bmatrix}b \\d \\ \end{bmatrix}=\vec{B},\begin{bmatrix}e \\f \\ \end{bmatrix}=\vec{C}\)と置くと
\(x=\frac{det(\vec{C},\vec{B})}{det(\vec{A},\vec{B})}\)
\(y=\frac{det(\vec{C},\vec{A})}{det(\vec{B},\vec{A})}\)
クラメルの公式ではxやyを行列式を利用して求めます。公式を見るとxの値は「ベクトルCとベクトルBが成す平行四辺形」を「ベクトルAとベクトルBが成す平行四辺形」で割ることで求まることになります。
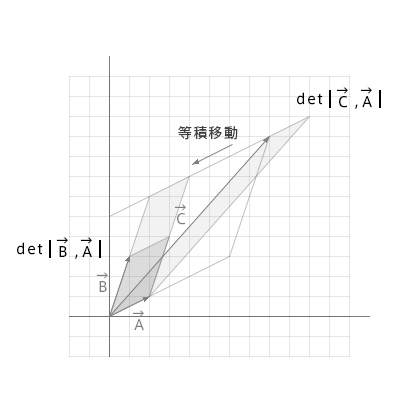
ではその様子を図形的に表してみます。
x成分
\(x=\frac{det(\vec{C},\vec{B})}{det(\vec{A},\vec{B})}\)
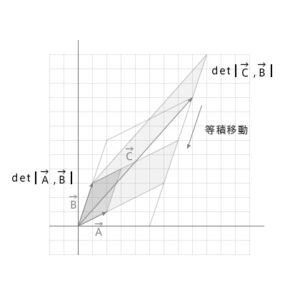
\(\vec{B}\)と\(\vec{C}\)の成す細長い平行四辺形を等積移動すると、\(\vec{A}\)と\(\vec{B}\)の成す平行四辺形を\(\vec{A}\)方向にスケールした平行四辺形になる。
y成分
\(y=\frac{det(\vec{C},\vec{A})}{det(\vec{B},\vec{A})}\)
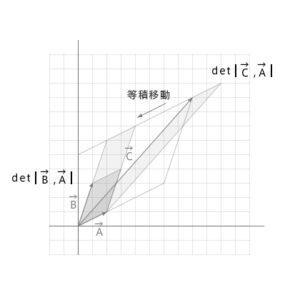
\(\vec{C}\)と\(\vec{A}\)の成す細長い平行四辺形を等積移動すると、\(\vec{A}\)と\(\vec{B}\)の成す平行四辺形を\(\vec{B}\)方向にスケールした平行四辺形になる。
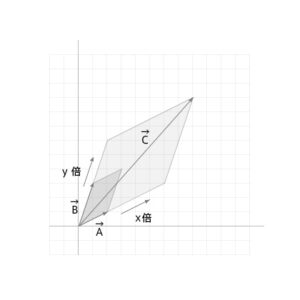
上の図から\(\vec{A}\)と\(\vec{B}\)の成す平行四辺形をそれぞれの方向にx倍、y倍にスケールしたものが\(\vec{A}x+\vec{B}y=\vec{C}\)の平行四辺形になることがわかると思います。
ベクトルの方向に伸びた平行四辺形を等積移動させて基本となる平行四辺形で割った値がそれぞれxとyになるということになりますね。
3次元のクラメル式
3次元でのクラメル式は計算量は多くなりますが、平行四辺形が平行六面体になるだけで概念は同じです。
\(x+y+z = 9\)
\(2x+3y-2z = 5\)
\(3x-y+z = 7\)
\(\begin{bmatrix}1 \\2 \\3 \\ \end{bmatrix}x +
\begin{bmatrix}1 \\3 \\-1 \\ \end{bmatrix}y +
\begin{bmatrix}1 \\-2 \\1 \\ \end{bmatrix}z =
\begin{bmatrix}9 \\5 \\7 \\ \end{bmatrix}\)
\(\begin{bmatrix}1 \\2 \\3 \\ \end{bmatrix}=\vec{A},
\begin{bmatrix}1 \\3 \\-1 \\ \end{bmatrix}=\vec{B},
\begin{bmatrix}1 \\-2 \\1 \\ \end{bmatrix}=\vec{C},
\begin{bmatrix}9 \\5 \\7 \\ \end{bmatrix}=\vec{D}\)
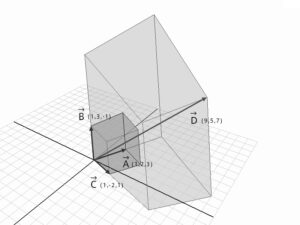
こうしてみるとエレガントな公式ですね。