
物を投げるときに最大飛距離になるための角度というのは経験的に45度となんとなく知られていることだと思いますが、どうしてそうなるか計算してみます。
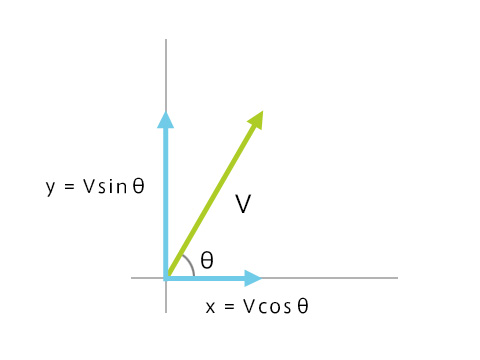
初速をV、角度をθ、重力をgとして砲弾を撃つとします。速度を分解すると図のようになる。
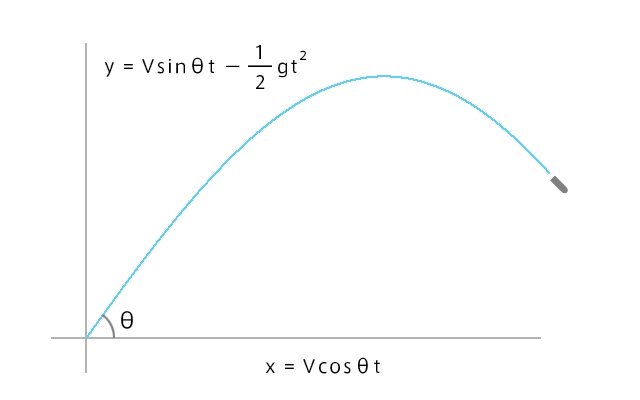
距離と高度のグラフ。Y軸は重力の公式。
\(x=Vcosθt\)・・・①
\(y=Vsinθt-\frac{1}{2}gt^2\)・・・②
砲弾が落下するときy = 0になるので
\(Vsinθt-\frac{1}{2}gt^2=0\)
\(t(Vsinθ-\frac{1}{2}gt)=0\)
となります。t = 0 または\(Vsinθ-\frac{1}{2}gt=0\)の時に y = 0になるということです。
t = 0 は砲弾を撃った時なので、落下した時は
\(Vsinθ-\frac{1}{2}gt=0\)
となります。式を変形して
\(t=\frac{2Vsinθ}{g}\)
これを①の式に代入すると
\(x=\frac{2V^2cosθsinθ}{g}\)
二倍角の公式より\(sin2θ = 2sinθcosθ\)なので
\(x=\frac{2V^2sin2θ}{g}\)
これが落下した時のxの値になります。この式の値が最大になるのはsin2θが最大になる時。sinは90度が最大の値(=1)となるので、2θ=90度の時になる。というわけでθは45度ということになります。

