とあるデザイナーのテクニカルノート

数学ノート

放物線で目標に当てる角度を求める

公開 更新

砲弾を目標に命中させるための角度を計算です。

初速をV、時間を t として目標の座標(x, y)を通過する式を考えます。

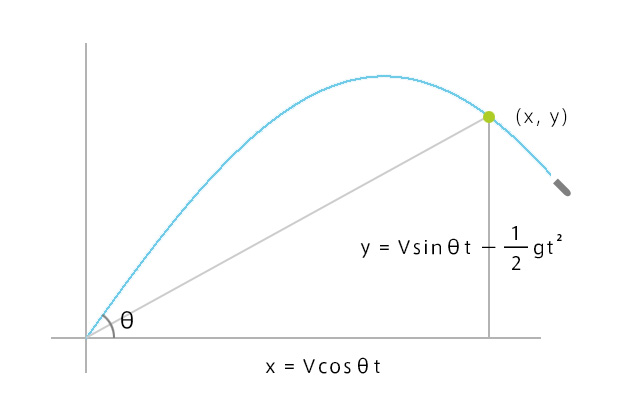
x, y それぞれのt秒後の座標を表した式はこうなります。縦方向は重力の公式を使っています。

x=Vcosθtx=Vcosθt・・・① y=Vsinθt−12gt2y=Vsinθt-\frac{1}{2}gt^2・・・②

これらの式を使って軌道の式を求めていきます。

①の式を変形して t=xVcosθt = \frac{x}{Vcosθ}

これを②の式に代入する y=VsinθVcosθx−12g(xVcosθ)2y=\frac{Vsinθ}{Vcosθ}x-\frac{1}{2}g(\frac{x}{Vcosθ})^2

三角比の関係式から、 tanθ=sinθcosθtanθ=\frac{sinθ}{cosθ}

1+tan2θ=1cos2θ1+tan^2θ=\frac{1}{cos^2θ}

代入して、軌道の式ができる y=tanθx−gx22V2(1+tan2θ)y=tanθx-\frac{gx^2}{2V^2}(1+tan^2θ)

軌道の式が出来たので、これをtanθの二次関数の式に変形していきます。二次関数の式ができれば解の公式で答えを計算することが出来ます。

P=gx22V2P=\frac{gx^2}{2V^2}として整理すると、

y=tanθx−P(1+tan2θ)y=tanθx-P(1+tan^2θ) y=tanθx−P−tan2θPy=tanθx-P-tan^2θP

両辺をPで割ると yP=xPtanθ−1−tan2θ\frac{y}{P}=\frac{x}{P}tanθ-1-tan^2θ tan2θ−xPtanθ+yP+1=0tan^2θ-\frac{x}{P}tanθ+\frac{y}{P}+1=0

tanθの二次関数の式になるので、解の公式−b±b2−4ac2a\frac{-b±\sqrt{b^2-4ac}}{2a}を使ってtanθを求める。 判別式D=b2−4acD=b^2-4acが0以上なら解があり、0以下なら解なし（弾が目標に届かない）ということになる。

判別式の係数はそれぞれ a=1a=1 b=−xPb=-\frac{x}{P} c=yP+1c=\frac{y}{P}+1

となるので、これで判別式の値を計算する。解が得られたら、解の公式を使ってtanθの値を求め、アークタンジェントでθが求まる。以下、Pythonコードでの計算

import math

G = 9.8 # 重力加速度

V = 800.0 # 初速[m/s]
y = 5000.0 # 高度[m]
x = 4000.0 # 距離[m]

b = -1 * (2 * V * V * x) / (G * x * x)
c = 1 + (2 * V * V * y) / (G * x * x)

# 判別式
D = b * b - 4 * c

if(D >= 0):
    # 解がある場合
    tanTheta0 = math.atan((-b - math.sqrt(D)) / 2)
    tanTheta1 = math.atan((-b + math.sqrt(D)) / 2)

    # 鋭角を選ぶ
    theta = min(tanTheta0, tanTheta1)

    print('Angle: ' + str(math.degrees(theta)) + '°')
    # Angle: 53.16906385467215°
    
    # 到達するまでの時間を計算する
    # x = VcosΘt
    # t = x / (VcosΘ)
    t = x / (V * math.cos(theta))
    print('Time: ' + str(t) + 's')
    # Time: 8.340897747064375s

初速800m/sの砲弾で距離4000m、高度5000mの目標を撃つ場合、角度を53.16906°で撃てばその放物線は目標を通過します。到達までにかかる時間は8.34秒となる。

大きく打ち上げて当てる場合

プログラムのコード内ではmin()によって鋭角を選んでいますが、max()に変えて鈍角を選べば大きく打ち上げて当てる軌道になる。

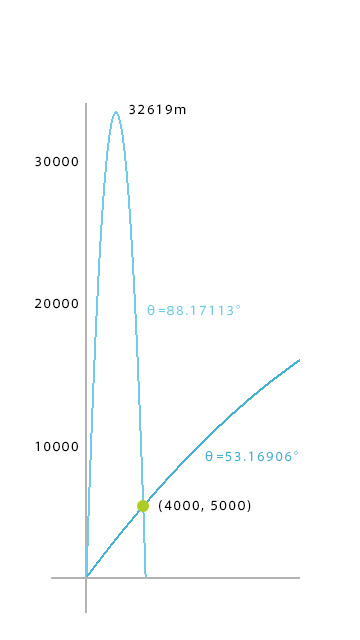
直撃で撃つと8.34秒後に目標に到達し、フライで撃つと高度32619mに到達した後、落下して目標に到達します。到達までにかかる時間は156.67秒と長くなります。

三角関数放物線解の公式重力

← 記事一覧へ