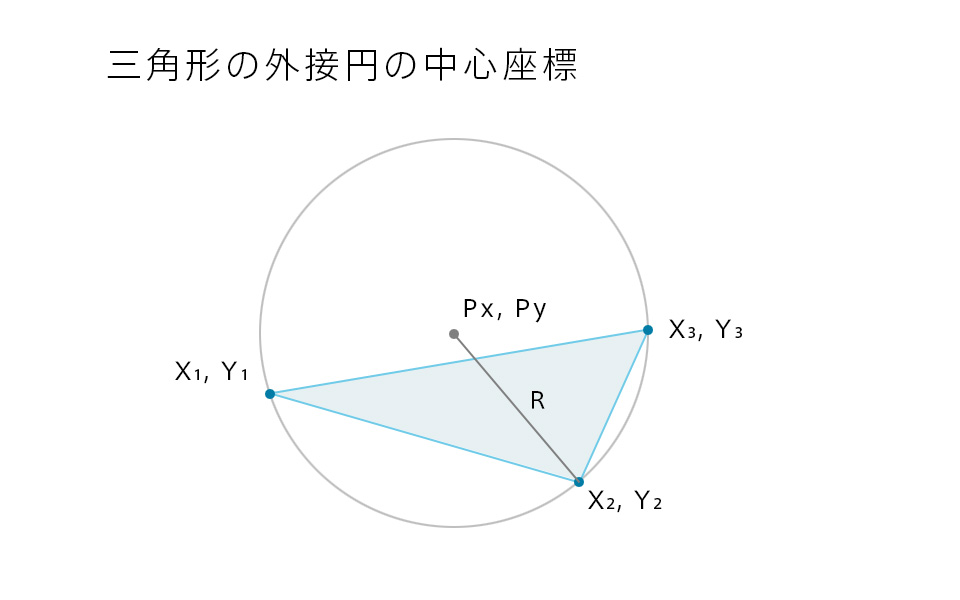
ピタゴラスの定理から
\((x_1 – Px)^2+(y_1 -Py)^2=R^2\)・・・①
\((x_2 – Px)^2+(y_2 -Py)^2=R^2\)・・・②
\((x_3 – Px)^2+(y_3 -Py)^2=R^2\)・・・③
①-②
\((x_1 – Px)^2 – (x_2 – Px)^2 + (y_1 – Py)^2 – (y_2 – Py)^2 = 0\)
まとめると
\(-2(x_1 – x2)Px – 2(y_1- y2)Py + x_1^2 – x_2^2 + y_1^2 – y_2^2 = 0\)
\(2(x_1 – x2)Px + 2(y_1- y2)Py = x_1^2 + x_2^2 + y_1^2 – y_2^2\)・・・④
同様に①-③は
\(-2(x_1 – x_3)Px – 2(y_1– y_3)Py + x_1^2 – x_3^2 + y_1^2 – y_3^2 = 0\)
\(2(x_1 – x_3)Px + 2(y_1– y_3)Py = x_1^2 – x_3^2 + y_1^2 – y_3^2\)・・・⑤
この二つの式④と⑤は連立方程式なので、二元一次方程式のクラメル式を使う
\(a_1x + b_1y = c_1\)
\(a_2x + b_2y = c_2\)
のとき
\(x = \frac{c_1b_2 – c_2b_1}{a_1b_2 – a_2b_1}\)
\(y = \frac{a_1c_2 – a_2c_1}{a_1b_2 – a_2b_1}\)
で求まるので、
\(a_1=2(x_1 – x_2)\)
\(b_1=2(y_1 – y_2)\)
\(a_2=2(x_1 – x_3)\)
\(b_2=2(y_1 – y_3)\)
\(c_1=(x_1^2 – x_2^2 + y_1^2 – y_2^2)\)
\(c_2=(x_1^2 – x_3^2 + y_1^2 – y_3^2)\)
と当てはめていけば答えは
\(Px = \frac{(x_1^2 – x_2^2 + y_1^2 – y_2^2)(y_1 – y_3) – (x_1^2 – x_3^2 + y_1^2 – y_3^2)(y_1 – y_2)}{2(x_1 – x_2)(y_1 – y_3) – 2(x_1 – x_3)(y_1 – y_3)}\)
\(Py = \frac{(x_1^2 – x_3^2 + y_1^2 – y_3^2)(x_1 – x_2) – (x_1^2 – x_2^2 + y_1^2 – y_2^2)(x_1 – x_3)}{2(x_1 – x_2)(y_1 – y_3) – 2(x_1 – x_3)(y_1 – y_3)}\)
となります。